Un metodo grafico per la moltiplicazione

…un gioco grafico per eseguire le moltiplicazioni tra numeri a due o a tre cifre, noto come moltiplicazione vedica…

I bambini trovano questo gioco grafico molto interessante, e presenta notevoli vantaggi. Lo consiglio perchè:

– può essere proposto ai bambini a partire dalla seconda o terza di scuola primaria, anche se non sanno ancora moltiplicare con grandi numeri, perchè consente di esercitare l’addizione e le tabelline , e anche il contare, il tutto con la possibilità di autocontrollo dell’errore (basta confrontare il risultato con quello una calcolatrice 🙂 )

– naturalmente può essere proposto poi ai bambini e ai ragazzi della scuola secondaria, come variante del procedimento classico di moltiplicazione, o anche come “prova”

– è un esercizio che migliora le capacità di orientamento spaziale e l’ordine

– è molto gratificante anche in termini estetici

– fa sentire molto bravi in matematica, trovandosi in grado di lavorare anche con grandi numeri.

______________

Cominciamo con l’esempio più semplice, e moltiplichiamo 12 x 32 =

Per il 12 tracciamo una riga orizzontale in alto (corrispondente alla prima cifra 1)

e due righe orizzontali in basso corrispondenti alla cifra 2:

Poi  tre linee verticali corrispondenti alla cifra 3 del 32:

e, più a destra, due linee verticali corrispondenti alla cifra 2 del 32:

Ora delimitiamo alcune specifiche zone del nostro bel disegno isolando due angoli, così:

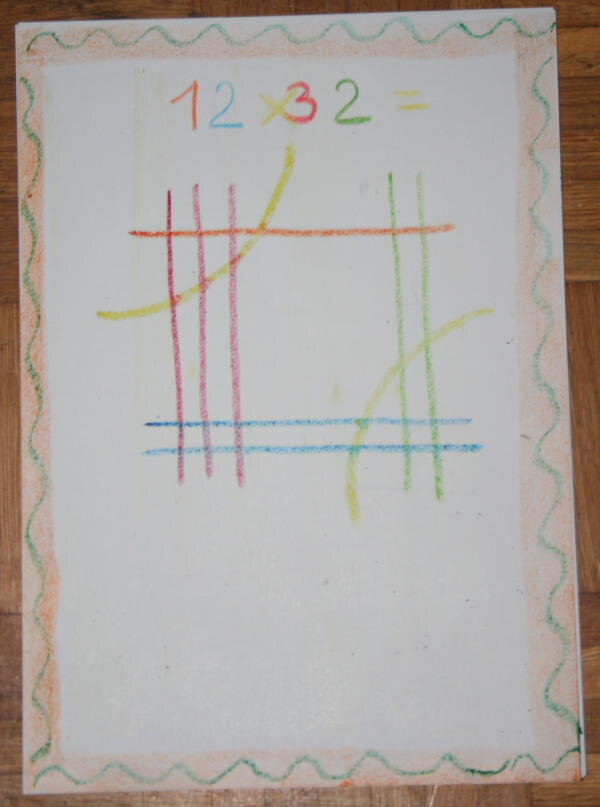
e contiamo disegnando un puntino in corrispondenza dei punti di intersezione delle linee, per ognuna delle tre zone delimitate (i due angoli e la zona centrale):

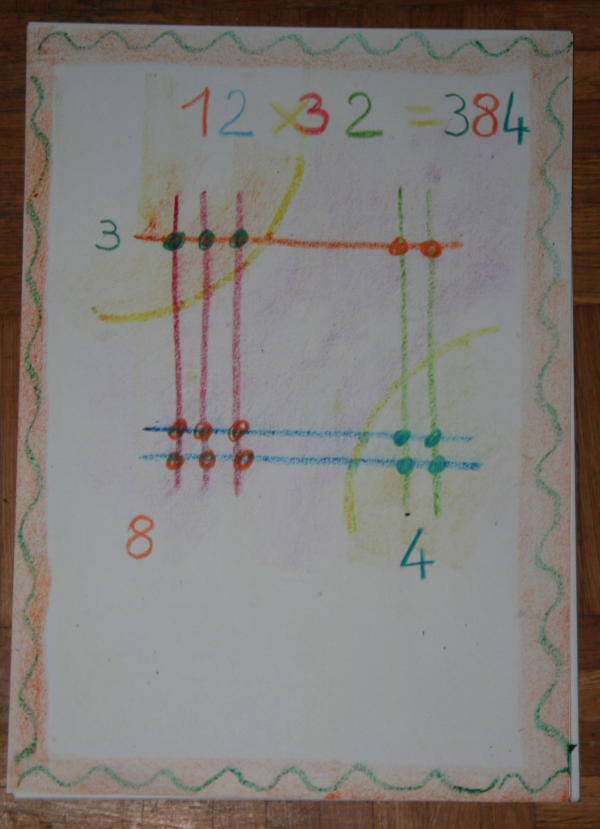
Controlliamo con la calcolatrice, e sì: 12 x 32 fa proprio 384 !

Questo esempio è scelto appositamente perchè contiene solo le cifre 1 2 e 3, ma il gioco grafico funziona con qualsiasi cifra… se il conteggio dei puntini dà risultati a due cifre, però, occorre aggiungere un ulteriore passo alla procedura.

Moltiplichiamo ora 46 x 53

Per prima cosa tracciamo le linee orizzontali corrispondenti al 46, e quelle verticali corrispondenti al 53, come spiegato sopra:

Poi delimitiamo le tre aree del disegno:

e contiamo i puntini in corrispondenza di ogni punto di intersezione delle linee, divisi per area:

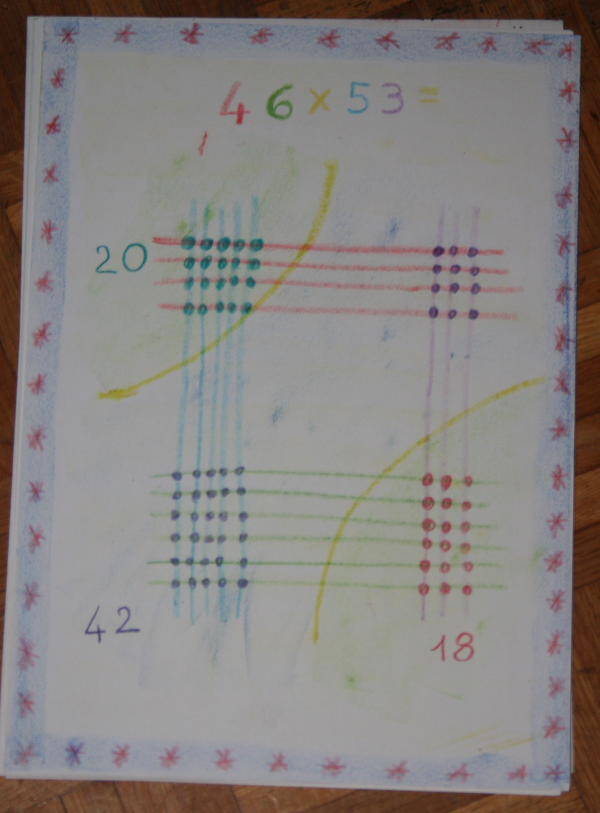
Abbiamo 20, 42 e 18. Come possiamo fare?

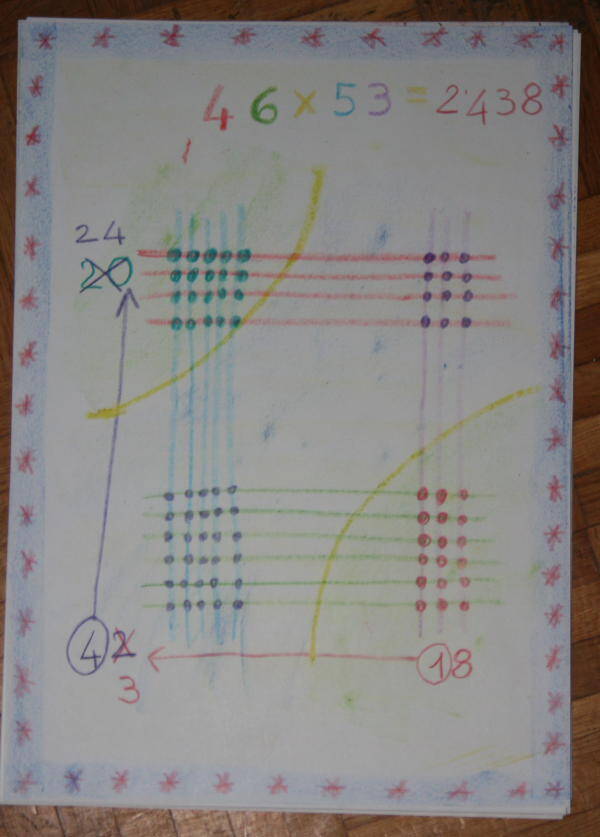
Partiamo dal 18, lasciamo l’8 al suo posto,  togliamo l’1 e lo spostiamo avanti, verso il 42. 42 +1=43

Del 43 lasciamo il 3 al suo posto e spostiamo avanti il quatto, verso il 20.

20+4 = 24

e 46 x 53 = 2.438

Giochiamo ora con cifre ancora più grandi, il primo esempio è 312 x 131 =

In questi casi, dovendo moltiplicare tra loro due numeri di tre cifre, le aree vanno divise così:

Contiamo, i punti di intersezione presenti in ogni areea, e scriviamo a lato il numero corrispondente:

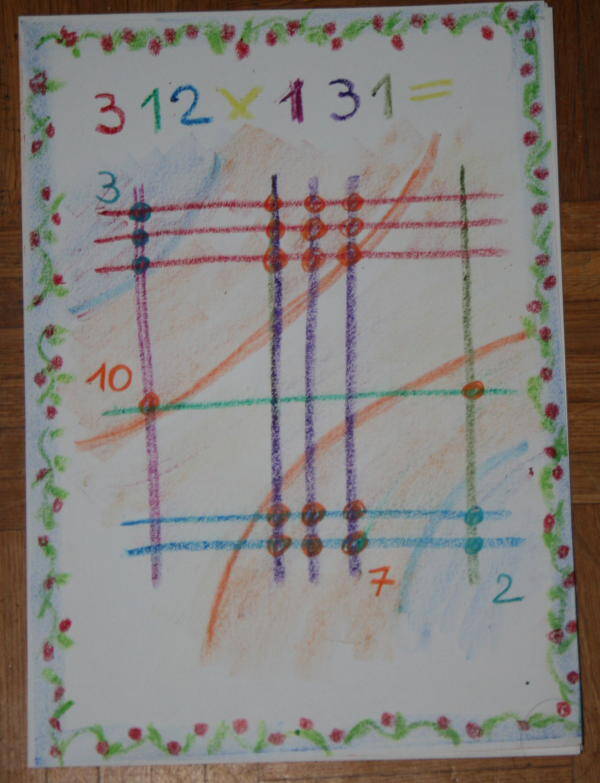
Come spiegato sopra le cifre che compongono il 10 vanno separate: lo 0 resta al suo posto, l’1 va ad aggiungersi al 3, che diventerà 4:

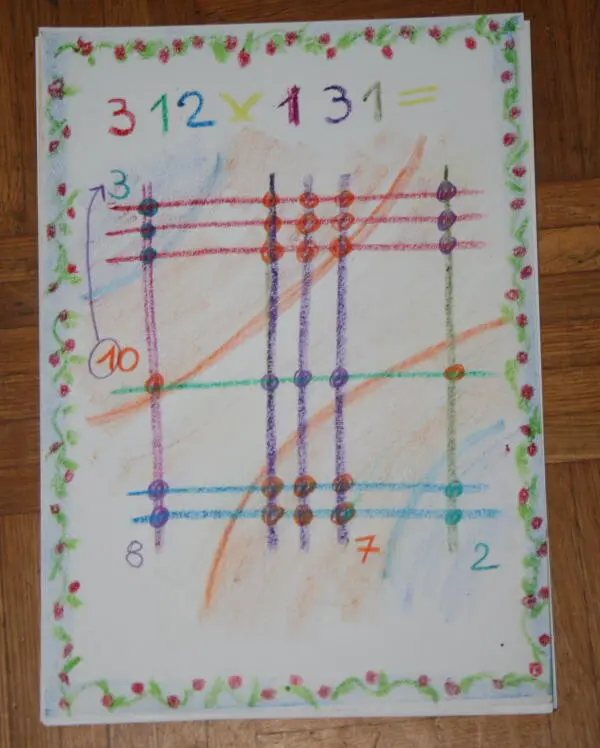
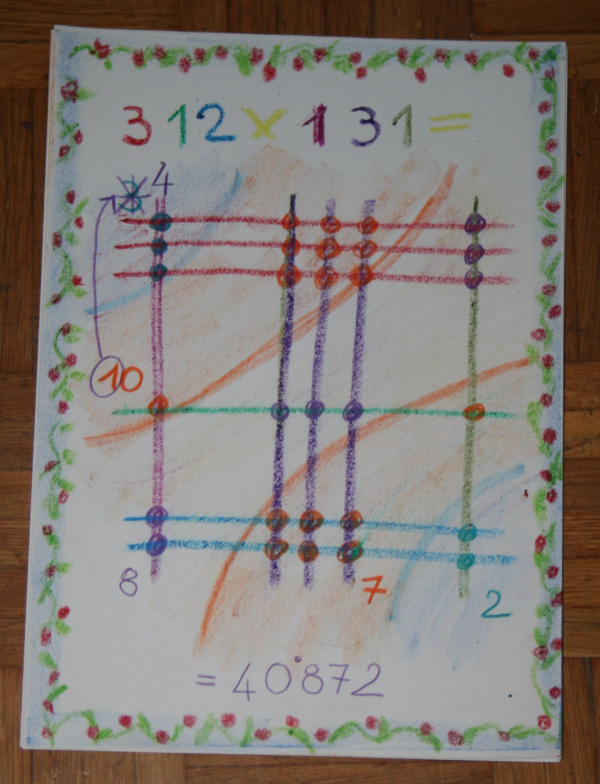
E il risultato sarà 40.872

Utilizzando cifre più alte, il bambino sarà stimolato a mettere in atto strategie diverse per contare i puntini, e senza dover dire nulla in proposito, presto deciderà da solo di utilizzare le tabelline, ad esempio così:

Per ottenere il risultato, dovrà spostare, a partire dal 18, ogni prima cifra ed aggiungerla al numero che sta davanti, così:

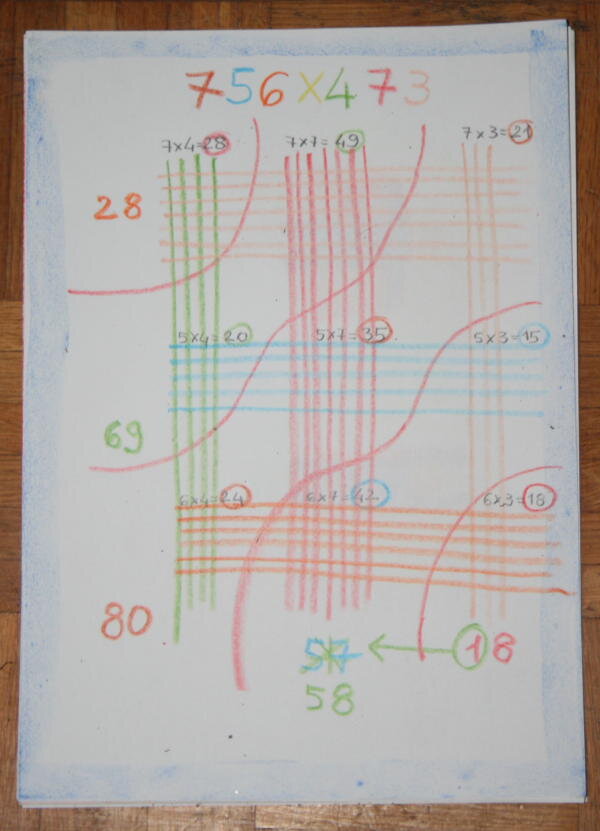
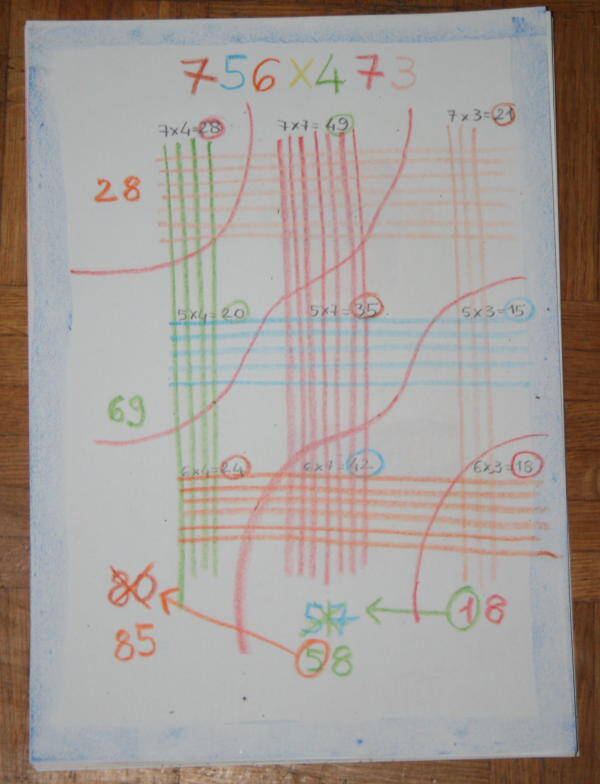
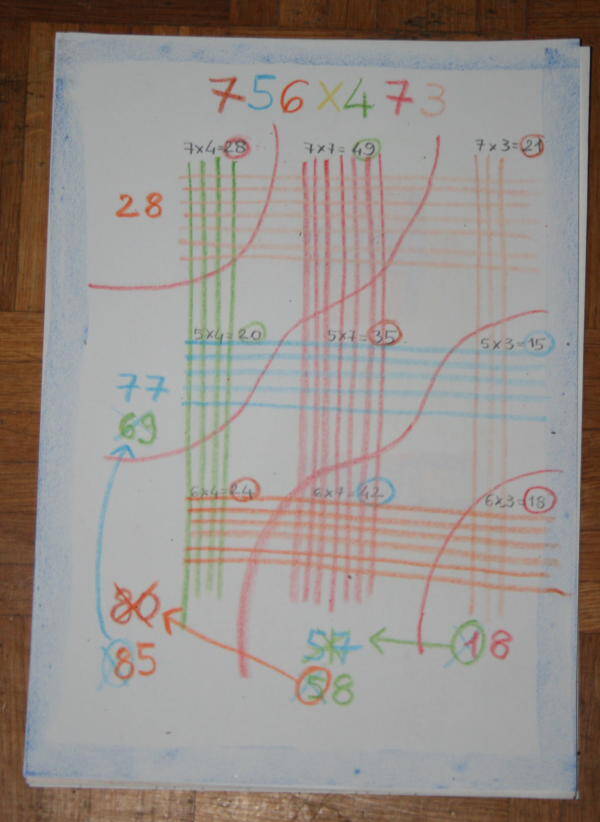
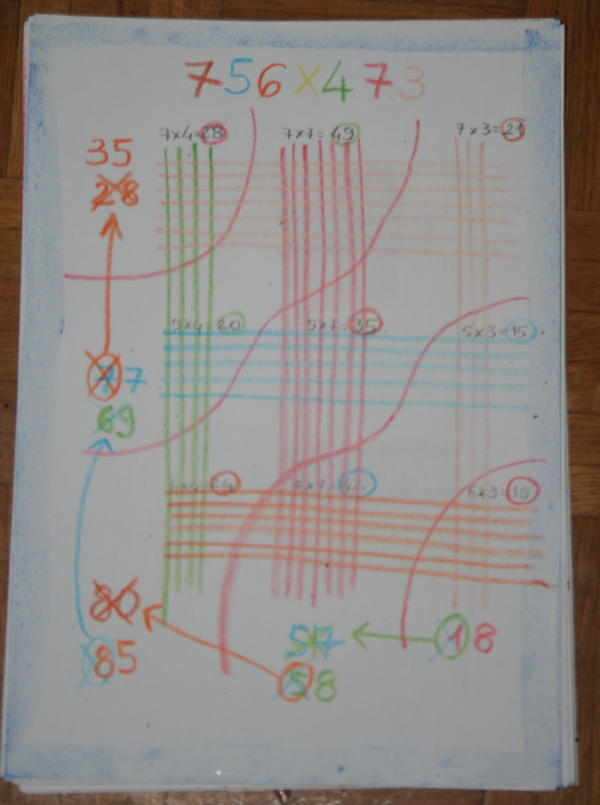
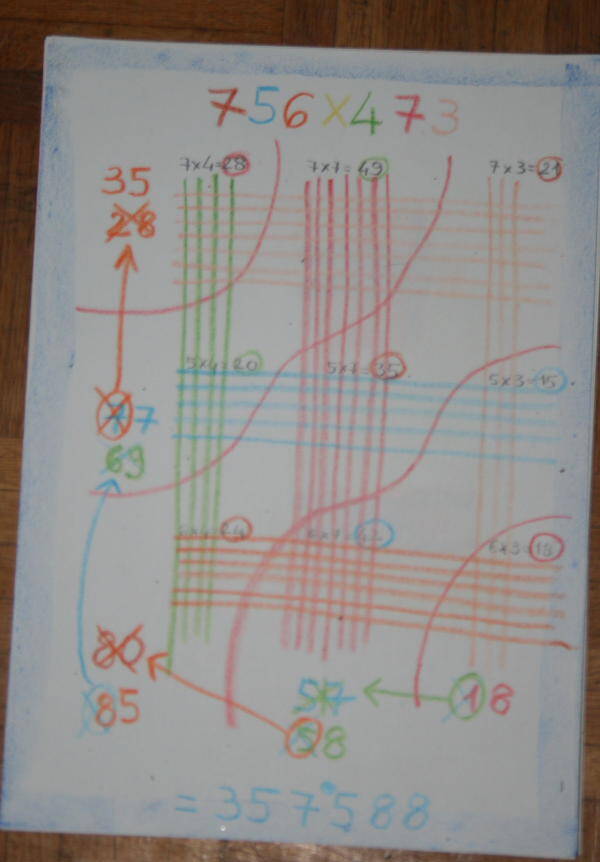
ottenendo il risultato corretto di 357.588

Ho usato spesso a scuola questo semplice gioco grafico per eseguire le moltiplicazioni, esercitare il calcolo orale, l’addizione e stimolare la memorizzazione delle tabelline, ma non sapevo si trattasse della “moltiplicazione vedica“, in questo video chiamata “moltiplicazione cinese“:

Nel web ne parlano, tra gli altri:

http://www.lanostra-matematica.org/

http://areeweb.polito.it/

http://www.softwaredidatticofree.it/

http://spicchidilimone.blogspot.it

visitando questi link troverete informazioni storiche su questo procedimento, varie curiosità, e anche un software…

The vedic

The vedic multiplication. Children find this graphic game very interesting. It has considerable advantages. I recommend it because:
– May be brought to the children in the second or third of primary school, although not yet know with multiply large numbers, because it allows you to exercise the addition and multiplication tables, and even the count,
all with the possibility of self-control error (simply compare the result with a calculator 🙂
– Of course it can be proposed then the older kids, as a variant of the traditional process of multiplication, or even as “proof”
– Is an exercise that improves the ability of spatial orientation and order
– It is also very rewarding in terms of aesthetics
– It makes you feel very good at math, being able to work well with large numbers.

______________

The vedic multiplication
Let’s start with the simplest example, and we multiply 12 x 32 =

For 12 we draw a horizontal line at the top (corresponding to the first number 1):

and two horizontal lines at the bottom corresponding to number 2:

Then three vertical lines corresponding at the number 3 of 32:

and, more to the right, two vertical lines corresponding at the number 2 of 32:

Now we delimit some specific areas of our beautiful design by isolating two angles:

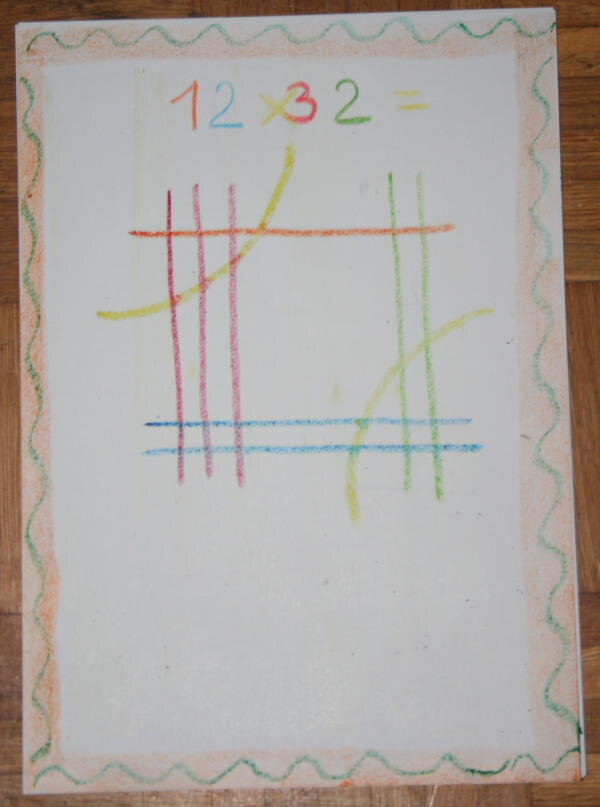
and we count plotting a point at the points of intersection of the lines, for each of the three zones demarcated (the two corners and the central area):

We check with the calculator, and yes: 12 x 32 does just 384!

This example was chosen specifically because it only contains the numbers 1, 2 and 3, but the graphic game works with any number … if the count of dots gives results in two numbers, however, we must add another step to the procedure.

The vedic multiplication

Now multiply 46 x 53

First we draw the horizontal lines corresponding to the 46, and the vertical corresponding to 53, as explained above:

Then we delimit the three areas of drawing:

and we count the dots in correspondence to each point of intersection of the lines, divided by area:

We have 20, 42 and 18. How can we do?

We start from the 18,
8 to leave the place,
we remove the 1 and we move it forward, towards 42.
42 + 1 = 43

43:
leave 3 in place
and move forward the four, towards 20.
20 + 4 = 24

and 46 x 53 = 2,438

The vedic multiplicationThe vedic multiplication
Let’s play now with even bigger numbers, the first example is 312 x 131 =

In these cases, having to multiply together two three-digit numbers, the areas should be divided so:

We count, the intersection points in each areea, and we write the number corresponding to the side:

As explained above, the numbers that make up the 10 should be separated: 0 stays in place, the 1 to be added to the 3, which will become 4:

And the result will be 40,872

Using higher figures, the child will be encouraged to implement different strategies to count the dots, and without having to say anything about it, soon will decide on its own to use multiplication tables, such as:

To get the result, you will have to move, starting from 18, each first number and add it to the number that is in front, as well:

getting the correct result of 357 588