Tavola con asticine dell’addizione e tavole di controllo stampabili. Il lavoro necessario a calcolare qualsiasi addizione si incentra sempre intorno al 10. Le addizioni parziali dei gruppi possono rimanere al di sotto della decina, raggiungerla o superarla. Per completare l’esercizio col tavoliere delle asticine, si offre un materiale scritto che conduce il bambino alla memorizzazione necessaria per il calcolo rapido.
In questo articolo trovi la descrizione dettagliata di tutte le tavole per l’addizione predisposte dalla Montessori, la tombola delle addizioni, i cartellini ed i moduli da compilare; mentre trovi tutto il materiale pronto per la stampa qui:
Il tavoliere delle asticine è in due versioni:
– piccola
– grande.
Oltre al tavoliere il materiale comprende tutte le tavole di controllo previste da Maria Montessori, compresa la tombola dell’addizione:
– moduli per l’esercizio scritto
– cartelli delle operazioni per le addizioni
– tavola I: questa tavola rappresenta tutte le combinazioni che si possono effettuare con i moduli per l’esercizio scritto
– tavola per il passaggio dalla Tavola I alla Tavola II
– tavola II: in questa tavola dell’addizione i riquadri sono disposti in modo che tutti i 10 risultino sulla stessa linea
– tavola per il passaggio dalla Tavola II alla tavola III
– tavola III, che si legge come la tavola pitagorica. Le due linee direttrici della cornice ricalcano la successione della serie naturale dei numeri da 0 a 9
– tavola IV
– tavola V
– tavola VI: la tombola dell’addizione.
Questa è la tavola con asticine per l’addizione:

Moduli per l’esercizio scritto
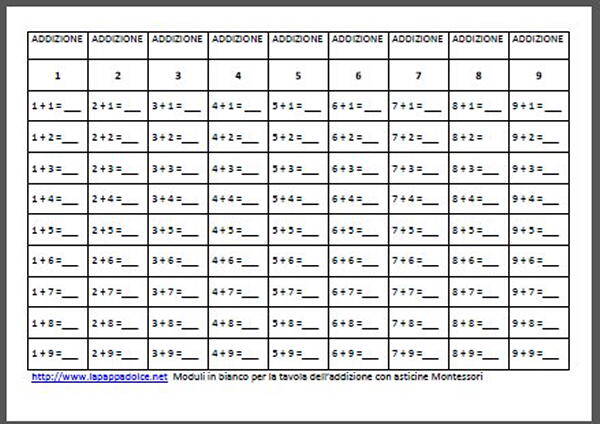
Nei moduli per l’esercizio scritto avremo sulla colonna di sinistra (primo addendo) sempre lo stesso numero (da 1 a 9), che viene sommato successivamente coi numeri da 1 a 9 (secondo addendo, nella colonna centrale). A destra si scrivono i numeri che rappresentano i totali. Dopo la stampa ritagliate i moduli lungo le linee verticali.
Questo materiale per gli esercizi scritti conduce il bambino ad impadronirsi di tutte le possibili combinazioni intorno al 10, necessarie e sufficienti da memorizzare. Stampatene tutte le copie che il bambino desidera.
Esercizi per l’addizione
Questi cartellini contengono tutte le combinazioni possibili, che rientrano nelle tavole dell’addizione, ed a parte, tutti i risultati corrispondenti:
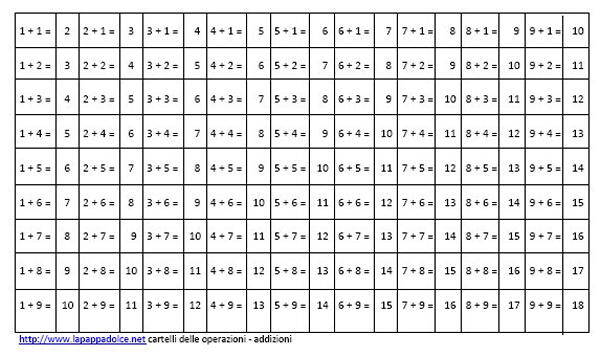
cartelli delle operazioni
Prima tavola dell’addizione – Tavola I
Questa tavola rappresenta tutte le combinazioni che si possono effettuare con i moduli per l’esercizio scritto.
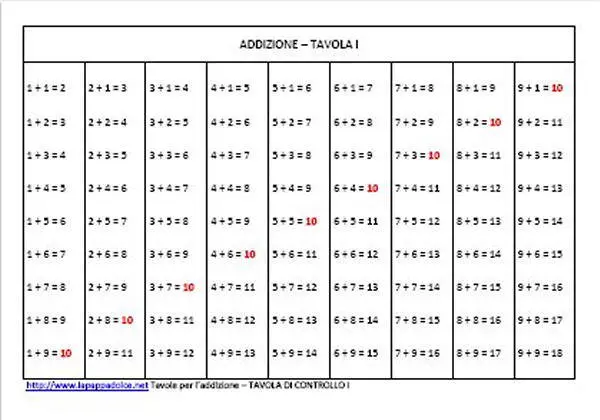
In essa ogni numero da 1 a 9 risulta addizionato con la serie dei numeri da 1 a 9.
Osservando la tavola, si vede che in ogni colonna è sempre presente un 10 come totale. Nella prima colonna (quella dell’1) il 10 è l’ultimo totale ottenuto, il penultimo nella colonna del 2, il terzultimo nella colonna del 3 ecc.. , mentre occupa la prima posizione nella colonna del 9.
Passaggio dalla tavola I alla tavola II
Il 10, nella tavola I, risulta sempre composto dall’unione di quegli stessi gruppi che il bambino ha avuto modo di conoscere fin da quando lavorava con le aste numeriche, quando, attraverso vari spostamenti, formava aste tutte di lunghezza 10 così:
9+1=10
8+2=10
7+3=10
6+4=10.
Sappiamo che 5+5=10 non è possibile con le aste numeriche per la presenza nella serie di una sola asta del 5: in realtà potremmo eseguire l’operazione 5×2, facendo ruotare l’asta di 180° gradi.
Le rimanenti combinazioni
4+6=10
3+7=10
2+8=10
1+9=10
sono semplicemente l’inverso delle combinazioni precedenti.
Disporre di aste rigide che si possono spostare per formare aste di valore 10 chiarisce il fatto che le successive combinazioni si rifanno alle precedenti e fa risaltare la differenza che esiste tra le nove combinazioni considerate nel loro complesso e la necessità di dislocare gli elementi che costituiscono le prime quattro combinazioni per poter concretizzare le ultime quattro.
Le combinazioni rappresentano il fatto più importante. Prendiamo ad esempio la combinazione 3+7=10. Se su questa combinazione si interviene con il dislocamento dei pezzi componenti cambiandoli in 7+3=10, risulta sempre la stessa combinazione, anche se sotto un altro aspetto, quasi come succede per una stessa moneta vista nel suo dritto e nel suo rovescio.
Ciò che occorre memorizzare, quindi, è la combinazione, ed ogni combinazione di gruppi diseguali di presenta doppia, dal punto di vista della posizione dei termini che la compone. Questo “duplicato inverso” può essere eliminato in una tavola semplificata, nella quale siano presenti tutte le possibili combinazioni, dove il necessario è ciò che è sufficiente:
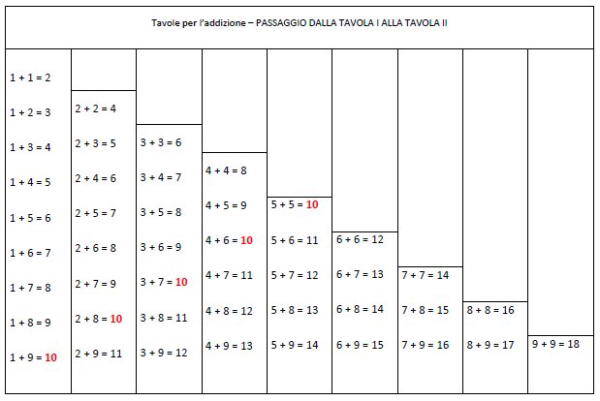
Per il passaggio dalla Tavola I alla Tavola II nelle scuole Montessori si utilizzano oggi dei rettangoli di cartoncino che vengono utilizzati per coprire via via le combinazioni ripetute sulla Tavola I: ne risulta che la tavola si presenta suddivisa in due parti triangolari. Soltanto in quella in basso a sinistra si possono leggere le 45 combinazioni rimaste. Tuttavia, per ottenere la Tavola II, dovremo idealmente tagliare in strisce verticali le combinazioni rimaste, per riallinearle in modo che tutte le addizioni con 10 per totale si trovino sulla stessa riga.
Seconda tavola dell’addizione – Tavola II
Nella seconda tavola dell’addizione i riquadri sono disposti in modo che tutti i 10 risultino sulla stessa linea.
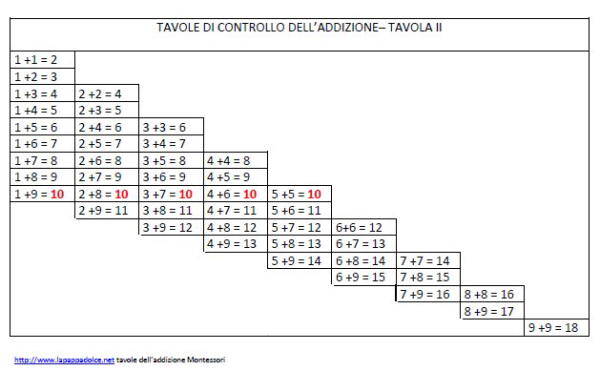
In questa tavola si trovano tutte le combinazioni dei gruppi che non raggiungono la decina, che si trovano al di sopra della linea in cui i risultati sono uguali a 10; tutte le combinazioni dei gruppi che superano la decina si trovano invece al di sotto della linea.
Nella Tavola II i riquadri organizzati secondo la linea del 10 offrono questo schema generale: in ogni riga sono presenti le combinazioni i cui totali risultano uguali.
Possiamo contrassegnare con colori meno accesi o con un carattere tipografico più piccolo, i duplicati delle combinazioni che è possibile eliminare alla scopo di ottenere quelle fondamentali. Le scomposizioni si verificano più volte ripetute con termini invertiti e, siccome si distinguono le ripetizioni, contrassegnandole con un colore più chiaro (ad esempio), si vede che esse vanno aumentando di numero dalla seconda colonna in avanti; vale a dire che ci si imbatte in un doppione nella colonna del 2, in due in quella del 3, ecc… e in otto nella colonna del 9.
Nella Tavola II, ogni colonna ha inizio con la combinazione in cui i due addendi sono fra loro uguali: 1+1 2+2 3+3 ecc…, e le altre combinazioni si svolgono (ma il 9+9 inizia e conclude la colonna) verso il basso.
Tutte le combinazioni della Tavola I si trovano nella Tavola II, procedendo a ritroso obliquamente e passando, in tal modo, attraverso tutte le colonne, fino alla prima.
Al di sopra della diagonale, cioè sopra la linea degli addendi uguali, si ritroverebbero le combinazioni ripetute in senso inverso (contrassegnate con colore pallido).
Se dalla Tavola I si eliminano dunque i duplicati, otteniamo una tavola semplificata contenente tutte le possibili combinazioni: questa Tavola II si può leggere e studiare come la tavola pitagorica per la moltiplicazione.
Leggendo le addizioni rimaste in ciascuna colonna, si vede che esse cominciano sempre con un numero addizionato a se stesso.
C0sì, ad esempio, considerando la colonna col 4+4:
– troviamo poi 3+4=7 (che si può leggere anche 4+3=7) nella colonna precedente e nella sua riga immediatamente superiore (salendo di una posizione in diagonale, insomma)
– nella colonna ancora più a sinistra (quella del 2) e nella riga ancora più in alto (salendo cioè in diagonale di un’altra posizione), troviamo 2+4=6 (che si può leggere anche 4+2=6).
– avvalendosi della proprietà commutativa dell’addizione, il bambino che lavora alle combinazioni del 4 troverà quelle non presenti (perchè già eliminate) rispettivamente nelle colonne del 3 del 2 e dell’1, dove il 4 è presente come secondo addendo.
La stessa cosa si osserva per tutti i numeri, procedendo obliquamente da destra a sinistra.
Per eseguire tutte le combinazioni di un dato numero partendo dalla minore, ad esempio tutte le addizioni relative al 3:
– partiamo da 1+3 della prima colonna
– proseguiamo in obliquo verso destra, di colonna in colonna, scendendo sempre di una riga: 2+3 3+3
– giunti a 3+3 si prosegue verticalmente sulla stessa colonna.
Terza tavola dell’addizione – Tavola III
Trascriviamo, uno sotto l’altro, colonna dopo colonna, i totali delle addizioni presenti nella Tavola I:
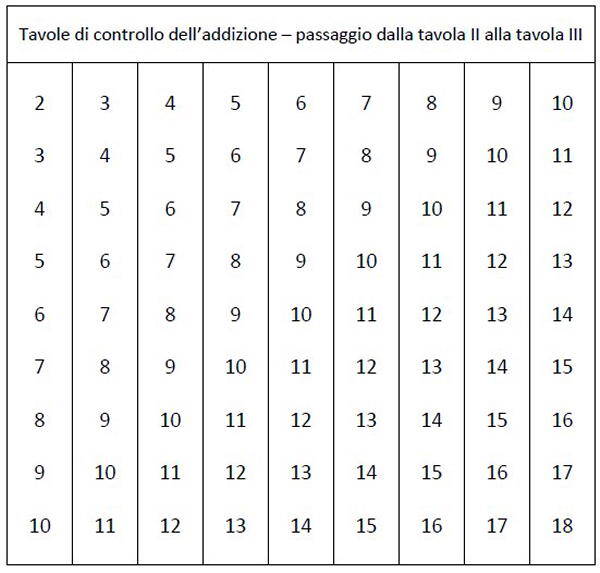
Costruiamo poi una cornice contenente la serie dei numeri da 1 a 9, prendendo lo zero per angolo. Si ottiene così questa tavola:
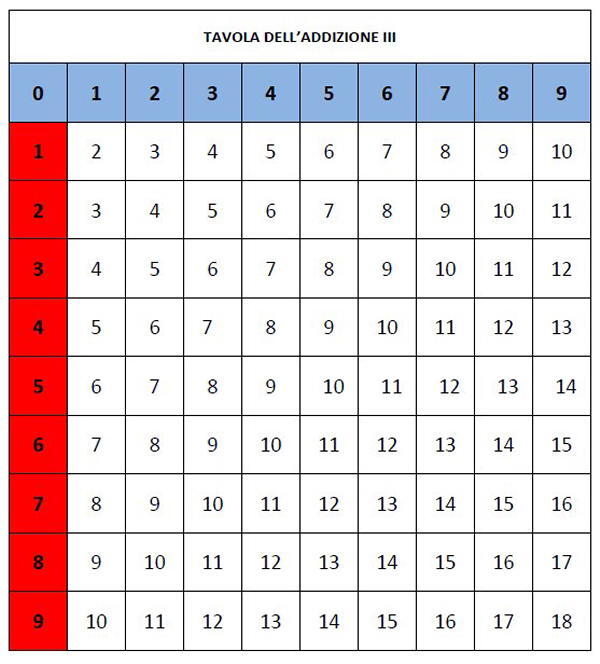
La Tavola III si legge come la tavola pitagorica: per esempio 8+5=13. Le due linee direttrici della cornice ricalcano la successione della serie naturale dei numeri da 0 a 9.
Lungo la diagonale si incontrano via via i doppi dei numeri presenti nella cornice, e fuori della diagonale non c’è altro che la ripetizione simmetrica delle addizioni presenti in ciascuna delle due metà. Per questo motivo basta imparare a memoria soltanto metà della tavola, cioè 45 combinazioni.
Quarta tavola dell’addizione – Tavola IV
Possiamo ridurre la Tavola III in questo modo:
– nella tavola, ogni numero da 1 a 9 si conclude, al termine delle rispettive righe, con il suo doppio.
– si vedono inoltre i numeri uguali incasellati in allineamenti ascendenti e discendenti tra loro paralleli e perpendicolari alla diagonale principale
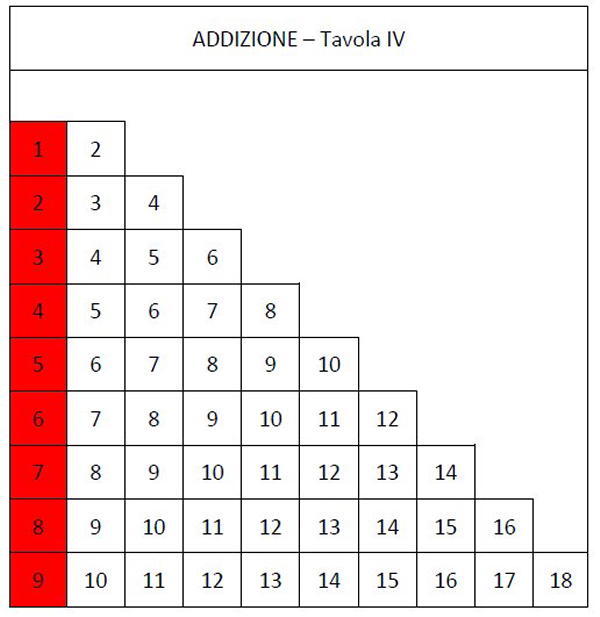
Per poter leggere la Tavola IV si procede verso destra fino a raggiungere il doppio del numero di partenza; se il totale dell’addizione è superiore a quel doppio (e questo accade quando il secondo addendo è maggiore del primo), si scende verticalmente fino alla riga che indica il livello del secondo addendo.
Prendiamo ad esempio l’addizione 4+7:
– si procede fino al doppio del 4 (4 x 2=8)
– si scende verticalmente fino alla riga del 7: il totale è 11.
Se desideriamo addizionare 5+8, partiamo allo stesso modo dal doppio del 5 (10) e poi scendiamo verticalmente fino alla riga dell’8, e troveremo il 13.
E’ evidente che, per eseguire ad esempio la somma 8+5, per la proprietà commutativa, opereremo in maniera che il primo addendo sia quello minore, cioè il 5.
Bisogna però dire che il bambino trova molto facilmente il totale in questo modo: punta i due addendi sulla striscia verticale, sposta poi le due dita orizzontalmente verso destra finchè un dito raggiunge la diagonale che limita la tavola, e a questo punto scende verticalmente fino ad incontrare la riga orizzontale indicata dall’altro dito.
Quinta tavola dell’addizione – Tavola V
Eseguendo parecchie di queste addizioni sulla Tavola IV si osserva che i risultati incontrati lungo la diagonale principale sono sempre numeri pari, e che quelli lungo la diagonale immediatamente al di sotto e parallela sono dispari. Perciò, queste due serie di numeri bastano ad indicare ogni possibile totale di addizioni entro il 18. Possiamo quindi ridurre la Tavola IV in questo modo:
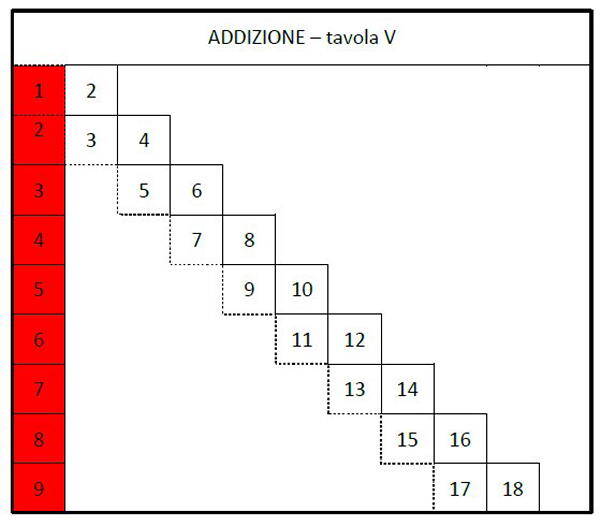
ottenendo la Tavola V.
Prendiamo come esempio l’addizione 5+8
– si procede orizzontalmente fino ad incontrare i rispettivi doppi, cioè 10 e 16
– si percorre la diagonale con direzione convergente, raggiungendo il 12 nello scendere, e il 14 nel salire
– il risultato si trova nella casella che sta tra il 12 ed il 14, sulla diagonale dei numeri dispari: 13
Prendiamo ora ad esempio l’addizione 3+7:
– arrivati al doppio 6+14 si procede in senso contrario
– sulla diagonale troviamo la casella del 10: questa volta il totale, essendo pari, si trova proprio sulla diagonale principale.
Prendiamo poi ad esempio l’addizione 3+9:
– avanziamo tra il 6 e il 18
– le dita si incontrano su un numero comune che si trova sulla diagonale: 12.
L’uso di due bastoncini per parte, che vengono opportunamente separati, dà a questo esercizio l’aspetto di gioco.
Dopo molti esercizi, il bambino potrà arrivare ad alcuni interessanti punti di coscienza:
– la somma di due numeri pari è un numero pari
– la somma di un numero pari e di un numero dispari è un numero dispari
– la somma di due numeri dispari è un numero pari.
Inoltre, la somma di due numeri è uguale alla media dei loro doppi. Infatti, intendendo per media aritmetica “la somma di due o più numeri divisa per il numero di essi” avremo ad esempio:
4+6= (4×2) + (6×2) x 1/2 = [2 x (4+6)] :2 = 10
Tavola dell’Addizione VI – Tombola dell’addizione (o Tavola con tombolini)
Oltre a queste cinque tavole di confronto, viene usata poi una sesta tavola con 81 totali mobili: è la Tombola dell’addizione.


