La dimostrazione del teorema di Pitagora col metodo Montessori utilizzando le tre tavole.

La dimostrazione del teorema di Pitagora col metodo Montessori
Le neuroscienze ci dicono che la comprensione della matematica presenta aspetti sia geometrico-percettivi sia simbolico-linguistici ed è necessario allenare il cervello a usare contemporaneamente entrambe le aree cerebrali.
Spesso la matematica è presentata ai bambini in modo puramente “linguistico”, come una lista di istruzioni da memorizzare. La memoria linguistica è molto potente e durevole, quindi i bambini inizialmente imparano con poco sforzo, ma quando la quantità di formule da memorizzare diventa eccessiva, la matematica diventa per loro materia arida e incomprensibile.
Per questo è necessario insegnare la matematica prima di tutto attraverso stimoli di tipo percettivo-sensoriale, soprattutto attraverso le mani, perché le aree cerebrali che ci permettono i movimenti fini sono molto vicine a quelle che ci fanno percepire le forme geometriche e le quantità approssimate.
Il materiale usato per la presentazione è offerto da:

I due testi fondamentali per l’insegnamento della matematica col metodo Montessori sono “Psicoaritmetica” e “Psicogeometria”, pubblicati per la prima volta nel 1934 in spagnolo quando l’autrice, a causa delle persecuzioni del fascismo, si trovava in esilio a Barcellona.
Le tesi esposte nelle due pubblicazioni, messe a confronto con le recenti scoperte delle neuroscienze, evidenziano marcati elementi di sintonia e attualità.
Prendiamo ad esempio il teorema di Pitagora: la sua formulazione “linguistica” recita che “in un triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti”.
Lo sforzo per la memoria linguistica è modesto, dunque si tende a partire dall’enunciato del teorema, presentando la sua dimostrazione, e poi si fanno seguire gli esercizi.
L’idea montessoriana è diversa, ed è molto semplice: bisogna partire dalle “cose”, cioè dalle rappresentazioni concrete degli oggetti geometrici.

“Non fu dalle cose, che i primi geometri trassero le loro conoscenze? Non furono corrispondenze e relazioni tra cose, che stimolarono qualche mente attiva e interessata a formulare degli assiomi e quindi dei teoremi?“
“Il modo con cui un concetto è stato compreso per la prima volta dagli esseri umani è il modo naturale per presentare quel concetto ai bambini”.
Maria Montessori
Sulla base di questa idea Maria Montessori introdusse nei due testi un’enorme quantità di materiali, che con la loro muta eloquenza permettono ai bambini di scoprire, in modo indipendente, la geometria e l’aritmetica.
“Nella scuola tradizionale lo studio del teorema di Pitagora rappresenta spesso un grosso scoglio da superare per i bambini, tanto che era chiamato “il ponte degli asini” (asino, si sa, era l’epiteto usato per gli studenti meno brillanti). Quando interrogati, gli studenti dovevano illustrare la dimostrazione del teorema disegnandola alla lavagna. Quelli che erano in grado di farlo avevano memorizzato sia il teorema sia la sua dimostrazione, ma erano in pochi quelli che l’avevano realmente compreso. Disegnando linee i bambini riproducono parallelogrammi equivalenti a quadrati, e rettangoli equivalenti a parallelogrammi e spiegano le ragioni dell’equivalenza. Le linee sulla lavagna si moltiplicano e alla fine il tutto diventa un labirinto che rispecchia il labirinto che c’è nella mente del bambino.
Anche se il postulato che recita: ‘Il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati costruiti sui sue altri lati’ è ben fissato nella mia mente, devo confessare che la prima volta che lo ho realmente compreso è stata quando ho visto la dimostrazione fatta con gli incastri delle tavole di Pitagora a bambini di 8 anni. Ma nella mente di tutte le persone a cui l’ho chiesto, il famoso teorema si riferisce soltanto ai quadrati. Nessuna altra figura geometrica gode dello stesso privilegio. Noi siamo in grado di utilizzare tutte le figure, purché esse siano equivalenti.
Questo è un esempio di cosa succede quando il bambino è liberato dalla schiavitù dei libri di testo e il suo potenziale intellettivo è stimolato e aiutato attraverso chiavi di conoscenza che gli permettono di investigare e creare con gioia ed entusiasmo.
I contenuti del programma scolastico sono coperti, ma se ne aggiungono molti altri ancora, e tutto con la piena comprensione e la gioia di imparare di una mente che ricerca e che vede le relazioni tra le cose.
Ciò accade non solo per quanto riguarda la geometria, ma anche per quanto riguarda il resto della matematica. Non è questo anche l’obiettivo dei sostenitori della nuova matematica?“
Mario Montessori – Communications 1 (1969)
La dimostrazione del teorema di Pitagora col metodo Montessori
Il materiale per il teorema di Pitagora è composto da 3 tavole con pezzi ad incastro blu, rossi, gialli e bianchi.
Le tre tavole rappresentano tre casi del teorema:
– primo caso (TAVOLA I): i due cateti sono uguali
– secondo caso (TAVOLA II): i due cateti stanno in proporzione 3:4 tra loro
– terzo caso (TAVOLA III): caso generale (la dimostrazione Euclidea).
La tavola 1 serve ad una dimostrazione del teorema a livello principalmente sensoriale.
La dimostrazione del teorema di Pitagora col metodo Montessori
TAVOLA I
i due cateti sono uguali

Per la prima dimostrazione abbiamo una cornice che corrisponde a uno spazio complesso, cioè:
– un triangolo rettangolo isoscele bianco
– lo spazio corrispondente ai quadrati costruiti sui tre lati:

Nel centro è collocato il triangolo bianco. Il resto del materiale è costituito dal quadrato diviso in otto triangoli a mezzo delle due diagonali e delle due mediane:

La dimostrazione del primo caso è estremamente intuitiva. In questo incastro:

– i due quadrati dei cateti sono divisi per mezzo della diagonale in due triangoli
– il quadrato dell’ipotenusa è diviso in quattro triangoli per mezzo di due diagonali.
Gli otto triangoli sono tutti uguali tra loro, quindi:
– i triangoli dei due cateti possono entrare nel quadrato dell’ipotenusa
– i quattro triangoli dell’ipotenusa possono riempire i due quadrati dei cateti.
Gli spostamenti sono molto divertenti, anche perchè i triangoli dei due cateti hanno lo stesso colore, mentre i quattro triangoli dell’ipotenusa hanno un colore diverso.
E’ facile vedere che i triangoli gialli e gli altri blu, fanno tra loro un quadrato col lato uguale al cateto di quello posto nel centro della cornice.
Gli altri 4 triangoli rossi, disposti in modo che i vertici siano tutti uniti al centro e le ipotenuse al di fuori, formano un quadrato, il cui lato corrisponde all’ipotenusa del triangolo che sta nella cornice.
Così gli 8 triangoli si possono collocare nella cornice riempendo tutto lo spazio, e dimostrando questo primo caso del teorema di Pitagora.
Con questa dimostrazione siamo partiti da un fatto noto, cioè il teorema di Pitagora, e da una cornice vuota che lo rappresenta; e abbiamo dimostrato il teorema riempiendo i vuoti della cornice.
________________
La dimostrazione del teorema di Pitagora col metodo Montessori
TAVOLA I – Presentazione 1
Esplorazione sensoriale del teorema di Pitagora
Mostriamo il materiale dicendo:
– “Le figure a destra della tavola mostrano i quadrati dei due lati del triangolo rettangolo isoscele, divisi a metà dalla linea diagonale, così da formare 2 triangoli interni per ogni quadrato, uno giallo e uno blu”
– “Il quadrato dell’ipotenusa è diviso da due linee diagonali , così da formare 4 triangoli interni rossi”
– “Gli 8 triangoli totali (2 gialli, 2 blu e 4 rossi) sono tutti identici, quindi con i triangoli gialli e blu dei quadrati dei cateti possiamo riempire lo spazio occupato dai 4 triangoli rossi del quadrato dell’ipotenusa”


– “Viceversa possiamo usare i 4 triangoli rossi per occupare lo spazio dei quadrati blu e giallo dei cateti”.

La sostituzione di questi differenti pezzi mobili è molto interessante, anche perchè presentano colori differenti. L’esercizio inoltre ricorda gli esercizi di equivalenza fatti con gli incastri delle frazioni.
______________________
La dimostrazione del teorema di Pitagora col metodo Montessori
TAVOLA I – Presentazione 2
Materiale:
– tavola del teorema di Pitagora I
Presentazione:
– osserviamo lo schema di figure a destra della tavola
– rimuoviamo il triangolo bianco e chiediamo ai bambini: “Che tipo di triangolo è?”. E’ un triangolo rettangolo isoscele

– rimettiamo al suo posto il triangolo bianco indichiamo i quadrati. Chiediamo ai bambini: “Cosa sono?” Sono quadrati
– diciamo ai bambini: “Oggi conosceremo insieme la relazione tra quadrati e triangoli.”
– indichiamo i lati del triangolo e facciamo notare che i quadrati adiacenti ai lati del triangolo hanno la loro stessa lunghezza
– Chiediamo: “Quale lato del triangolo ha la stessa lunghezza del triangolo grande rosso?” L’ipotenusa
– indichiamo l’ipotenusa e diciamo: “L’ipotenusa ha la stessa lunghezza del quadrato rosso”
– esaminiamo i pezzi per mostrare le loro equivalenze


– passiamo allo schema di figure a sinistra della tavola e diciamo: “Questi sono gli stessi quadrati divisi da diagonali. Ci sono molte equivalente tra le figure dello schema”
– rimuoviamo interamente il quadrato rosso (formato da 4 triangoli) e incoraggiamo i bambini a notare che è equivalente alla somma dei quadrati gialli e blu combinati
– nota altre equivalenze, ad esempio che il quadrato giallo è metà del quadrato rosso, come ne è la metà anche il quadrato blu

– al termine dell’esperienza, diamo la regola: “Nel triangolo rettangolo, la somma del quadrato costruita sui cateti è uguale al quadrato costruito sull’ipotenusa”.
______________________
La dimostrazione del teorema di Pitagora col metodo Montessori
TAVOLA I – Presentazione 3
Introduzione:
– diamo ai bambini qualche semplice informazione su Pitagora, dicendo che fu un grande matematico dell’Antica Grecia, nato nell’isola di Samo nel 500 aC. Egli fondò la sua scuola a Crotone (Italia meridionale), che era allora parte della Magna Grecia
– troviamo Pitagora nella linea del tempo.
Questa breve introduzione è molto utile perchè richiama il nome del materiale, cioè la tavola del teorema di Pitagora; inoltre il collegamento con la storia fa sentire ed apprezzare ai bambini il proprio legame con gli uomini del passato.
Presentazione
Primo passaggio: sostituzione dei pezzi:
– iniziamo con la tavola contenente tutti i pezzi già disposti nel modo corretto per dare una prima forte impressione

– togliamo tutti i pezzi dal primo schema

– prendiamo i pezzi dell’altro schema e mettiamoli nelle cornici del primo, cioè muoviamo i pezzi da un lato all’altro

Secondo passaggio:
– dallo schema nel quale i quadrati sono divisi dalle diagonali formando i triangoli colorati, togliamo i triangoli gialli e quelli blu. Chiediamo a un bambino di riempire i due quadrati dello schema a sinistra utilizzando i quattro triangoli rosso che formano il quadrato grande

– i triangoli rossi che erano sull’ipotenusa del triangolo bianco sono stati distribuiti in due quadrati posati sugli altri due lati (cateti) del triangolo bianco

– ora con i triangoli blu e gialli riempiamo lo spazio lasciato libero dai triangoli rossi: tutto ciò che era costruito sui cateti ora si trova sull’ipotenusa.
Applicazione del teorema:
– la somma dei quadrati costruiti sui cateti di un triangolo rettangolo è uguale al quadrato costruito sull’ipotenusa dello stesso triangolo.
Note:
– i triangoli dello schema sono tutti triangoli isosceli.
Scopo diretto:
– introduzione sensoriale al materiale
– preparazione per gli incastri seguenti
Età:
– dagli 8 anni.
Teorema di Pitagora col metodo Montessori
TAVOLA II
i due cateti sono in proporzione 3:4

Nell’incastro i tre quadrati sono riempiti con quadratini di tre diversi colori. Il loro numero è:
– nel quadrato del cateto minore 3² = 9
– nel quadrato del cateto maggiore 4² = 16
– nel quadrato dell’ipotenusa 5² = 25.
In questo caso speciale calcolando le lunghezze dei lati per se stesse, si ha il numero di quadrati che riempiono le superfici, cioè:
3 x 3 = 9 quadrati
4 x 4 = 12 quadrati
5 x 5 = 25 quadrati
e quindi 25 = 16 + 9.

Siccome i quadratini relativi al quadrato di ogni lato sono di colore diverso, si possono disporre a disegni vari i quadratini corrispondenti ai due cateti, nel quadrato dell’ipotenusa.
Allora gli spazi relativi ai quadrati dei due cateti restano riempiti coi quadratini relativi all’ipotenusa, e rimanono di colore uguale i quadrati dei cateti.
La dimostrazione del teorema di Pitagora col metodo Montessori
Tavola II – Presentazione 1
Il gioco degli spostamenti è evidente:
– i due quadrati dei cateti possono essere riempiti completamente con i quadratini dell’ipotenusa, diventando dello stesso colore
– il quadrato dell’ipotenusa può essere composto in due colori creando bei disegni.

Così rimane materialmente ed esteticamente dimostrata la relazione pitagorica cambiando i quadratini mobili negli spazi della cornice che si trova nel materiale.
Tavola II – Presentazione 2
Materiale:
– tavola del teorema di Pitagora II
Presentazione:
– rimuoviamo dalla tavola il triangolo bianco e chiediamo ai bambini: “Che tipo di triangolo è?” E’ un triangolo rettangolo scaleno
– diciamo: “Questa è un’altra dimostrazione della teoria di Pitagora”.
– diciamo: “In questa tavola i quadrati sono divisi in quadratini tutti uguali. Possiamo usarla per verificare che la somma dei quadrati dei lati è uguale al quadrato dell’ipotenusa. “
– chiediamo l’aiuto dei bambini per inserire tutti i quadratini blu e gialli nella cornice quadrato grande e i quadratini rossi nelle cornici dei quadrati medio e piccolo:

– chiediamo ai bambini cos’hanno scoperto e chiediamo se quello che abbiamo fatto con i quadratini colorati può essere scritto
– facciamolo insieme:
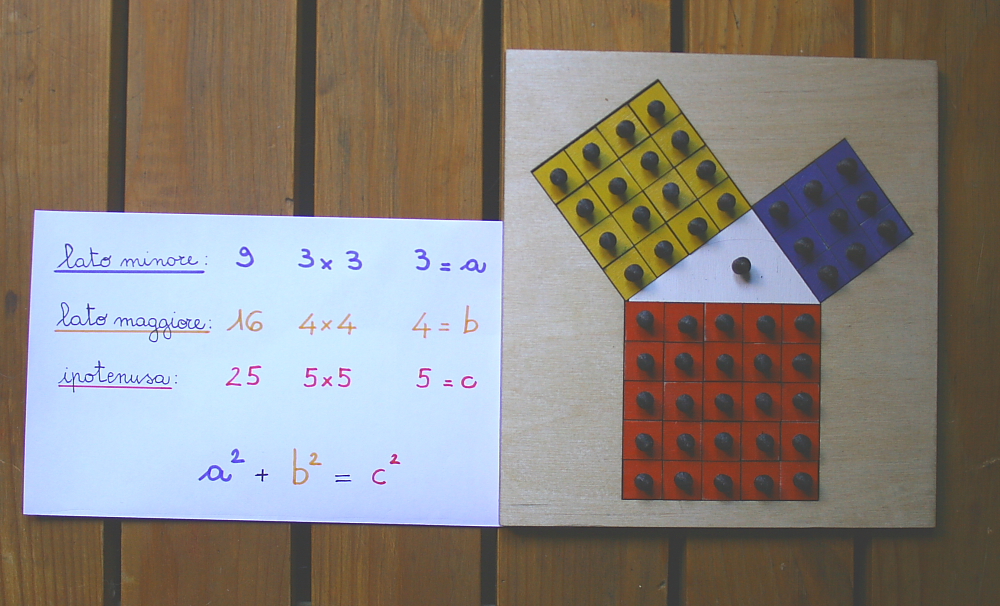
– dopo essersi esercitati con la tavola i bambini possono risolvere problemi detti a voce, ad esempio possiamo dare la misura dell’ipotenusa e di un lato di un triangolo, e i bambini devono trovare la lunghezza dell’altro lato.
La dimostrazione del teorema di Pitagora col metodo Montessori – Nota:
Si tratta della terna pitagorica. Una terna pitagorica è una terna di numeri naturali 



Tavola II – Presentazione 3
Materiale:
– tavola del teorema di Pitagora II
Presentazione:
– mostriamo il materiale e diciamo: “Qui i numeri magici sono 3, 4 e 5”
– “In questa figura i tre quadrati sono riempiti con piccoli quadratini tutti uguali e in differenti colori”
– con questo materiale il gioco delle sostituzioni viene spontaneo, per cui basta invitare il bambino a sperimentare il materiale in tutte le possibili combinazioni
– facciamo notare che i due quadrati costruiti sui due cateti (giallo e blu) possono essere interamente riempiti con i quadratini rossi del quadrato costruito sull’ipotenusa

– facciamo notare anche che i quadratini giallo e blu insieme possono riempire lo spazio occupato dal quadrato rosso
– facciamo notare che il triangolo bianco centrale è un triangolo rettangolo scaleno.
________________________
La dimostrazione del teorema di Pitagora col metodo Montessori – Tavola II – Presentazione 4
Materiali:
– tavola del teorema di Pitagora II: tavola nella quale i lati del triangolo sono in proporzione 3:4. In questo caso c’è un solo schema sulla tavola. Il triangolo bianco è un triangolo rettangolo scaleno.
Presentazione:
– per prima cosa contiamo i pezzi. Questa tavola aggiunge elementi di aritmetica agli elementi sensoriali. Evidenziamo che il triangolo bianco centrale è un triangolo scaleno
– togliamo dallo schema tutti i quadratini gialli e tutti i quadratini blu. Proviamo a riempire gli spazi vuotati con i quadratini rossi
– al termine ci troveremo con lo spazio per il quadrato dell’ipotenusa vuoto. Riempiamo questo spazio con i quadratini gialli e con quelli blu
– nel fare questa operazione si possono ottenere combinazioni di giallo e blu molto interessanti

– contiamo i quadratini. Possiamo scrivere il conteggio così:
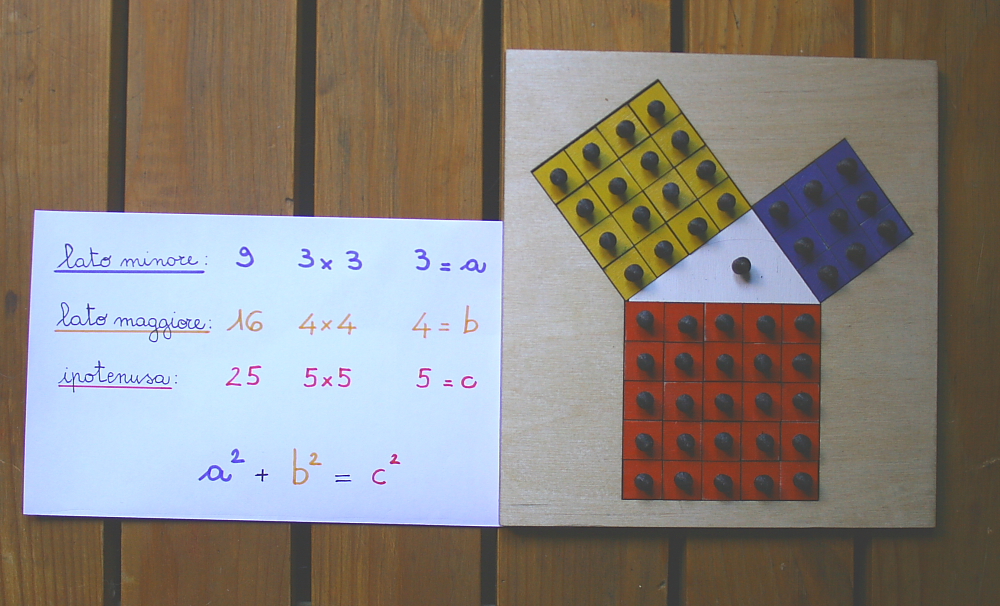
– la somma dei quadrati costruiti sui lati di un triangolo rettangolo è uguale al quadrato costruito sull’ipotenusa dello stesso triangolo.
Teorema di Pitagora col metodo Montessori
TAVOLA III
caso generale

In ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
Il materiale che serve a questa dimostrazione Il terzo incastro è di difficile descrizione e si presta a un notevole esercizio intellettuale.
Il materiale originale prevedeva una tavola 44 x 24 cm, con quattro incavi rettangolari ai due lati e al centro la cornice che, per la sua determinazione di forma, presenta appunto un teorema già stabilito, che bisogna dimostrare.
I pezzi mobili possono formare varie combinazioni per dimostrare vari principi del teorema, e cioè:
– due quadrilateri aventi base uguale e altezza uguale sono equivalenti
– due figure equivalenti a una terza figura sono equivalenti tra loro.
Occorre dimostrare che la somma dei due rettangoli equivale alla somma dei quadrati costruiti sui cateti. La dimostrazione materiale si fa con lo spostamento delle figure.
Nell’incastro in posizione normale:

– il quadrato dell’ipotenusa è diviso in due rettangoli
– il secondo lato è determinato dalle divisioni dell’ipotenusa, su cui cade l’altezza del triangolo abbassata dal vertice opposto.
Nel materiale troviamo anche due romboidi che presentano:
– un lato uguale al lato del quadrato piccolo
– un lato uguale al lato del quadrato grande
– un lato uguale all’ipotenusa.
L’altezza minore dei due romboidi corrisponde all’altezza (o lato minore) dei rettangoli.

L’altezza maggiore corrisponde ai lati dei quadrati dei cateti:

Non è necessario che il bambino conosca già tutte queste corrispondenze dimensionali: vedrà dei pezzi a incastro rossi blu e gialli, e semplicemente li sposterà inserendoli negli incavi della tavola.
A far ragionare il bambino sul teorema è il suo agire materialmente inserendo i pezzi mobili sui fondi della tavola, e non la conoscenza astratta delle corrispondenze dimensionali dei lati e delle altezze delle figure geometriche.
In questo modo l’esercizio diventa molto semplice e interessante, e il materiale si presta dare diverse dimostrazioni.
TAVOLA III – Presentazione 1

– Partiamo dall’incastro riempito normalmente:

– togliamo prima i due rettangoli dell’ipotenusa e mettiamoli nei lunghi incavi laterali della tavola
– facciamo scorrere verso il basso il triangolo bianco fino a che l’ipotenusa tocca il lato inferiore del quadrato. Rimane vuoto, al di sopra del triangolo, uno spazio che evidentemente equivale al quadrato. Questo spazio vuoto equivale evidentemente al quadrato. Esso ha la forma di uno strano poligono a sei lati, però prolungando la linea corrispondente all’altezza del triangolo, subito si capisce che lo spazio si può dividere in due romboidi, uno maggiore e uno minore.
– riempiamo lo spazio rimasto coi due romboidi giallo e blu: le due figure riempiono perfettamente lo spazio.

Vediamo così che è sempre lo stesso spazio riempito:
– prima con 1 triangolo + 2 rettangoli
– poi con 1 triangolo + 2 romboidi.
Questo dimostra che la somma dei due rettangoli (quadrato dell’ipotenusa) è equivalente alla somma dei due romboidi.
_____________________
TAVOLA III – Presentazione 2


Consideriamo poi i romboidi invece dei rettangoli, per dimostrare la loro equivalenza coi due quadrati sui cateti:
– cominciamo dal quadrato maggiore e partiamo dall’incastro in posizione normale:

– consideriamo lo spazio occupato dal triangolo e dal quadrato maggiore: per farlo togliamo i pezzi e vuotiamolo
– riempiamo lo spazio vuotato con il triangolo e il quadrato grande in posizione normale
– ora togliamo il quadrato del cateto maggiore (giallo)
– facciamo scorrere nello spazio vuoto il triangolo, fino a che il vertice del suo angolo retto si incastra nello spazio di un angolo retto lasciato vuoto dal quadrato: il cateto maggiore corrisponde al lato sterno del quadrato perchè tutti i lati del quadrato spostato sono uguali al cateto maggiore
– è evidente che lo spazio che resta vuoto dopo aver inserito il triangolo è equivalente al quadrato portato via. Questo spazio vuoto ha la forma di un romboide: uno dei suoi lati corrisponde all’ipotenusa e l’altro al lato del quadrato, cioè al cateto maggiore del triangolo
– inseriamo nello spazio il romboide grande giallo:

– allo stesso modo possiamo considerare anche lo spazio occupato dal triangolo e dal quadrato minore: per farlo togliamo prima il quadrato del cateto minore
– facciamo scorrere nello spazio vuoto il triangolo, fino a che il vertice del suo angolo retto si incastra nello spazio di un angolo retto lasciato vuoto dal quadrato: il cateto minore corrisponde al lato sterno del quadrato perchè tutti i lati del quadrato spostato sono uguali al cateto minore
– è evidente che lo spazio che resta vuoto dopo aver inserito il triangolo è equivalente al quadrato portato via. Questo spazio vuoto ha la forma di un romboide: uno dei suoi lati corrisponde all’ipotenusa e l’altro al lato del quadrato, cioè al cateto minore del triangolo
– inseriamo nello spazio il romboide piccolo blu:

_____________________
TAVOLA III – Presentazione 3
Con queste attività vogliamo dimostrare le equivalenze tra i romboidi e i rettangoli e tra i romboidi e i quadrati, utilizzando gli incavi lunghi che si trovano ai lati della tavola. Questi incavi dimostrano che i pezzi hanno la stessa altezza.
– Partiamo dall’incastro in posizione normale:

– togliamo i due rettangoli che insieme riempiono uno spazio uguale al quadrato costruito sull’ipotenusa e mettiamoli insieme con i rombi negli incavi di sinistra (i maggiori nell’incavo più largo e i minori in quello più stretto):

Vediamo come le figure incastrate hanno uguale altezza. Basterà poi far combaciare i pezzi secondo la base per verificare l’uguaglianza: dunque le figure sono a due a due equivalenti.
Torniamo poi nella disposizione normale dell’incastro e procediamo allo stesso modo con i quadrati:

Negli spazi paralleli di destra si possono disporre il quadrato grande in fila col romboide grande, disposto però in un altro senso (cioè il senso dell’altezza maggiore).
Allo stesso modo si possono mettere nell’incavo minore di destra il quadrato piccolo e il romboide piccolo: quadrato e romboide hanno la stessa altezza e affiancandoli possiamo verificare che hanno base uguale. Dunque i quadrati e i romboidi sono equivalenti.
I rettangoli e i quadrati, equivalenti ai romboidi, sono perciò equivalenti tra loro.
Il teorema risulta dimostrato.
_______________________
TAVOLA III – Presentazione 4
Materiali:
– tavola del teorema di Pitagora III

Presentazione:
– rimuoviamo i rettangoli rossi dal telaio
– facciamo scorrere il triangolo bianco verso il basso e posizioniamo il parallelogramma giallo e blu nel telaio. Facciamo notare ai bambini che i parallelogrammi sono equivalenti ai rettangoli rossi. Rimettiamo i pezzi com’erano nella posizione iniziale
– rimuoviamo il quadrato giallo e facciamo scorrere verso l’alto il triangolo bianco. Mettiamo il parallelogramma giallo nello spazio vuoto. Facciamo notare ai bambini che il parallelogramma giallo è equivalente al parallelogramma giallo. Rimettiamo i pezzi com’erano nella posizione iniziale
– rimuoviamo il quadrato blu e facciamo scorrere verso l’alto il triangolo bianco. Inseriamo nello spazio vuoto il parallelogramma blu. Facciamo notare ai bambini che il parallelogramma blu è equivalente al quadrato blu. Rimettiamo i pezzi com’erano nella posizione iniziale
– diciamo: “Ora sappiamo che i lati di una figura con lati uguali e base uguale sono equivalenti.”
– mostriamo quanto abbiamo detto posizionando il quadrato giallo accanto al parallelogramma giallo confrontando base e altezza
– diciamo ai bambini: “Dal momento che le figure gialle sono equivalenti e il parallelogramma giallo è equivalente al rettangolo rosso, possiamo dire che il quadrato giallo e il rettangolo rosso sono equivalenti?”. Sì
– dimostriamo che il quadrato blu è equivalente al parallelogramma blu.
– diciamo ai bambini: “Poiché il quadrato blu e il parallelogramma blu sono equivalenti, cosa possiamo dire del quadrato blu e del piccolo rettangolo rosso?” Sono equivalenti.
_________________________
Tavola III – Presentazione 5

La tavola III, per essere precisi, non dimostra tanto il teorema di Pitagora quanto la teoria di Euclide. Si tratta del famoso teorema del pons asinorum (ponte degli asini) della geometria euclidea che afferma: “Gli angoli opposti ai due lati uguali di un triangolo isoscele sono congruenti“. Si tratta, in sostanza, del contenuto della proposizione 5 nel libro I degli Elementi di Euclide.
Per prima cosa i bambini noteranno che il triangolo centrale dello schema della tavola è un triangolo rettangolo scaleno, uguale a quello usato nella tavola II.
I principi già studiati o suggeriti attraverso gli esercizi sensoriali con le altre tavole e che dimostrano il teorema sono:
– due quadrilateri che hanno base uguale e altezza uguale sono equivalenti
– due figure equivalenti a una terza figura sono equivalenti tra loro
– il quadrato formato sull’ipotenusa è diviso in due rettangoli. La divisione è fatta prolungando perpendicolarmente la linea che va dall’apice del triangolo bianco all’ipotenusa
– nel materiale sono compresi anche due romboidi, ognuno dei quali ha un lato uguale rispettivamente al quadrato grande e al quadrato piccolo dei lati del triangolo bianco, e l’altro lato uguale all’ipotenusa
– le altezze minori dei due romboidi corrispondono alle rispettive altezze (lati corti) dei rettangoli
– il lato maggiore corrisponde rispettivamente al lato del quadrato grande e del quadrato piccolo dei lati del triangolo.
Non è necessario che il bambino conosca tutte queste corrispondenze. Egli vede i pezzi colorati di un inserto e semplicemente lo sposta, mettendolo nelle cornici. Questa attività è ciò che dà al bambino l’opportunità di ragionare sul teorema, e non l’idea astratta delle corrispondenze e delle relazioni tra le figure.
__________________
TAVOLA III – Presentazione 6
Con questa tavola porteremo avanti due dimostrazioni:
– dimostrazione A, basata sul movimento della mano usata per scambiare i pezzi nelle cornici; questo porterà all’applicazione del concetto di equivalenza, in particolare l’equivalenza tra rettangoli e parallelogrammi e l’equivalenza tra quadrati e parallelogrammi
– dimostrazione B, basata sulle relazioni tra le linee nelle figure equivalenti.

Dimostrazione A:
– rimuoviamo i rettangoli rossi dalla cornice centrale. Proviamo a mettere i parallelogrammi giallo e blu (che si trovano nelle cornici laterali) al loro posto. Ai primi tentativi non ci riusciremo, ma se facciamo scivolare verso il basso il triangolo bianco il gioco è fatto. Questo dimostra l’equivalenza tra i rettangoli rossi e i parallelogrammi giallo e blu
– rimettiamo tutti i pezzi al loro posto. Ora lavoriamo con le figure blu
– proviamo a mettere il parallelogramma blu al posto del quadrato blu: non è possibile
– muoviamo il triangolo bianco verso l’alto e verso destra nello spazio del quadrato blu. Ora il parallelogramma blu potrà essere inserito senza problemi
– facciamo lo stesso con i pezzi gialli
abbiamo così dimostrato la qualità transitiva dell’equivalenza:
A=B
B=C
A=C proprietà transitiva
Dimostrazione B:
– prendiamo il più piccolo dei rettangoli rosi e mettiamolo nella cornice di sinistra con il parallelogramma blu. Lo spazio è lungo abbastanza per i due pezzi. La larghezza della cornice rappresenta rappresenta le altezze delle due figure: le due altezze quindi sono uguali
– mettiamo le due figure fianco a fianco per dimostrare che le basi sono uguali. Due parallelogrammi che hanno la stessa altezza e la stessa base sono equivalenti
– facciamo la stessa cosa con il rettangolo rosso grande e il parallelogramma giallo. Rettangoli e parallelogrammi con la stessa altezza e la stessa base sono equivalenti
– ripetere l’attività con i parallelogrammi e i quadrati blu e giallo. Ora useremo le cornici di destra
– mettendo i pezzi nelle cornici dimostreremo che le altezze sono le stesse
– controlliamo anche la lunghezza delle basi delle due figure affiancando i due pezzi tra loro
– parallelogrammi e quadrati con la stessa altezza e la stessa base sono equivalenti
La dimostrazione del teorema di Pitagora col metodo Montessori – Conclusione:
– prendiamo le figure blu e il rettangolo rosso più piccolo
– il parallelogramma blu ha la stessa altezza e la stessa base del quadrato e del rettangolo rosso. Quindi il quadrato e il rettangolo sono equivalenti
– prendiamo le figure gialle e il rettangolo rosso più grande: esse sono equivalenti.
La dimostrazione del teorema di Pitagora col metodo Montessori – Scopo:
– comprendere il teorema
– risolvere problemi in modo pratico (dopo i 10 anni)
La dimostrazione del teorema di Pitagora col metodo Montessori – Età:
– a livello sensoriale, dopo aver presentato le altre due tavole del teorema di Pitagora (8 anni)
– per applicazioni a problemi geometrici a partire dai 10 anni.
_________________________________
