Giochi logici per la terza classe – una raccolta di giochi logici e piccoli rompicapo per bambini della terza classe della scuola primaria.
Impossibile! Perchè?
Ciascuna delle seguenti frasi contiene qualcosa di assurdo. Invitiamo i bambini a cogliere l’assurdità ed a fornirne la spiegazione.
1. Ieri mattina ha preso a piovere e son tre giorni che non smette.
2. Il fruttivendolo coltiva il suo orto per metà a cavoli, metà a piselli e metà a insalata.
3. Camminando all’indietro quell’uomo non si avvide del muro finchè non vi ebbe battuto la fronte.
4. Luigi dichiara che non entrerà nell’acqua finchè non avrà imparato a nuotare.
5. Un vecchio, lamentandosi di non poter fare il giro completo di un parco perchè tale passeggiata lo affaticava troppo, si accontentava di fare il giro fino a metà.
L’ascensione della lumaca
Una lumaca sale un muro alto cinque metri. Ogni giorno sale tre metri e ogni notte ne discende due. Povera lumaca, quanta fatica!
Sapreste dire dopo quanti giorni la lumaca sarà giunta in cima al muro?
La lumaca sale il muro in tre giorni perchè il terzo giorno, giunta in cima al muro, non discende più.
I due recipienti
Un signore manda il proprio domestico al fiume, incaricandolo di raccogliere e portargli cinque litri di acqua. Gli consegna un recipiente di tre litri e uno di quattro litri.
Come fa il domestico ad eseguire l’incarico?
Il domestico riempie il recipiente da 4 l e, con questo, quello da 3 l. Vuota quest’ultimo e vi mette il litro d’acqua rimasto nel primo, che poi riempie di nuovo, portando così 4 + 1 = 5 l di acqua.
Come te la caveresti?
Se tu entrassi in una casupola molto buia per ripararti dal freddo, avendo in tasca un solo fiammifero, e in quel riparo ci fossero una lucerna ad olio, un vecchio giornale e un po’ di sterpi nel caminetto, cosa accenderesti per primo?
Il fiammifero, ovviamente.
Il contadino intelligente
Un contadino possedeva un campicello quadrato. A ogni vertice, subito oltre la cinta, era posto un albero che non gli apparteneva.
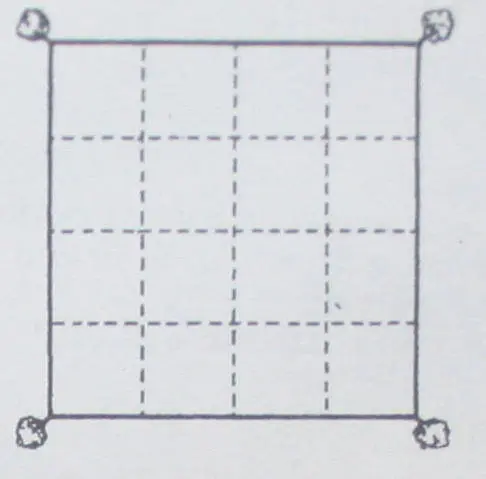
Volle raddoppiare la sua proprietà, mantenendole la forma quadrata.
Acquistò il terreno, ma non gli alberi, che rimasero al medesimo posto e oltre la cinta del suo nuovo campo.
Come fece?
Risposta
In questo modo l’estensione del campo è stata raddoppiata, senza toccare gli alberi:
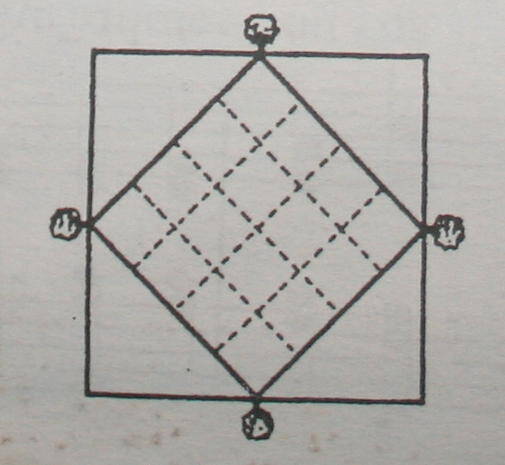
Diagonali magiche
Scriviamo in tre quadrati di nove quadratini l’uno le prime nove cifre della serie naturale dei numeri nell’ordine indicato dalle tre figure.
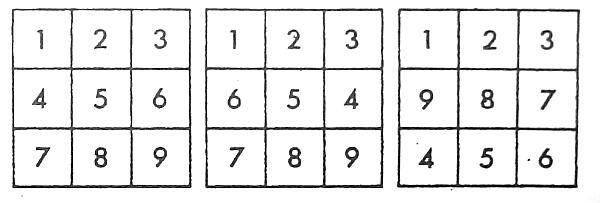
Sommiamo ora i numeri di ciascuna diagonale. Il totale sarà per tutte e sei le diagonali il numero 15. Queste diagonali si chiamano “diagonali magiche”.
La pesca magica
Ponete in un cappello, o in una scatola, alcune monete uguali. Prendetene una a caso e segnatela visibilmente con una matita colorata. Mostrate la moneta con il segno ai bambini e invitate poi uno di loro a magnetizzarla, tenendola ben serrata in pugno per qualche istante. Nel frattempo, bendatevi gli occhi, o ponetevi nella condizione di non poter pescare guardando. Tastate le monete che sono nel cappello (la “magnetizzata” compresa) e sarete subito in grado di riconoscerla al semplice tatto perchè questa sarà più calda delle altre tre per essere stata a lungo tenuta in mano.
L’alfabeto degli amici
Il direttore del gioco dice una lettera dell’alfabeto e lancia una pallina. Il bambino che la riceve è obbligato a tenere un discorsetto.
Se la lettera è M, dire ad esempio: “Io ho un amico che si chiama Mario, è modesto, abita a Milano; per la mia festa mi ha regalato una matita”.
Se la lettera è la P: “Io ho un amico che si chiama Paolo, è pietoso, abita a Palermo; per la mia festa mi ha regalato un pallone”.
Il bambino che non è pronto a rispondere paga pegno.
Quando, dove, come?
Invitiamo un bambino ad allontanarsi dalla stanza, in modo che non possa ascoltare quello che si dice. Gli altri bambini, in sua assenza, stabiliscono il nome di un oggetto, di un cibo, o altro, che l’assente deve indovinare al suo ritorno.
Fatta la scelta, l’assente è invitato a ritornare nella stanza. Egli rivolge, successivamente, a tre compagni le seguenti domande: “Come ti piace?”, “Dove ti piace?” e “Quando ti piace?”
I compagni rispondono con frasi che si riferiscono all’oggetto scelto. Se si tratta, poniamo, di una palla, gli interrogati possono rispondere:
“Mi piace grossa e colorata”
“Mi piace ai giardini pubblici”
“Mi piace quando siamo in tanti ad adoperarla”.
Se le tre risposte non bastano a far capire l’oggetto designato, si può rivolgere ad altri giocatori con qualche altra domanda, ad esempio:
“Tu la possiedi?”
“E’ di legno?”
“Dove si compera?”
Ma le domande non possono poi oltrepassare un numero preventivamente stabilito, che può essere di sei o sette. Se l’interrogante non indovina, torna ad allontanarsi dal gruppo. I suoi compagni scelgono il nome di un altro oggetto e il gioco riprende.
Se indovina, rientra nel gruppo ed è sostituito da un suo compagno estratto a sorte.
Gli espedienti di Menicone
Menicone, il mugnaio, aveva quel giorno un sacco di farina, una bilancia, e solo un peso da 2 kg. Arrivò Nena e gli chiese un chilo di farina.
“Prendine due chili” disse Menicone, “Un chilo non saprei come pesarlo”
“O un chilo, o non se ne fa niente!” ribattè Nena, e fece per andar via.
“No” disse Menicone, dopo un attimo di perplessità, “Farò come tu vuoi: te ne peserò un chilo”.
Come fece?
(Pesò 2 kg; poi divise la farina sui due piatti della bilancia in modo che si equilibrassero)
Dove?
Sai mettere in dieci secondi la mano destra in un posto dove non puoi mettere la sinistra?
(sul gomito sinistro)
Piripicchio piripacchio
Chi dirige il gioco stabilisce:
– alla parola piripicchio (ad esempio) mani sul banco
– alla parola piripacchio (ad esempio) mani in alto…
… ma dicendo “Piripicchio” o “Piripacchio” chi dirige il gioco fa il contrario di quanto ha stabilito, per indurre gli altri in errore. Naturalmente le due parole si alternano a piacere. Chi sbaglia paga pegno.
Fantasia di numeri
Come puoi ottenere 100 adoperando tutte e nove le cifre significative in ordine decrescente?
Così: (9 x 8) + 7+ 6 + 5+ 4 + 3 + 2 + 1 = 100
Indovina numero
Dettate queste cinque serie di numeri:
1 ______ 2 _____ 4 ____ 8 ____ 16
3 ______ 3 _____ 5 ____ 9____ 17
5 ______ 6_____ 6____ 10____ 18
7 ______ 7 _____ 7 ___ 11____ 19
9 _____ 10 ____ 12____ 12____ 20
11 ____ 11____ 13____ 13 ____ 21
13 ____ 14 ____ 14 ____ 14____ 22
15 ____ 15 ____ 15 ____ 15 ____ 23
17 ____ 18 ____ 20 ____ 24 ____ 24
19 _____ 19 ____ 21 ____ 25 ____ 25
21 ____ 22 ____ 22 ____ 26 ____ 26
23 ____ 23 ____ 23 ____ 27 ____ 27
25 ____ 26 ____ 28 ____ 28 ____ 28
27 ____ 27 ____ 29 ____ 29 ____ 29
29 ____ 30 ____ 30 ____ 30____ 30
31 ____ 31 ____ 31 ____ 31 ____ 31
Poi chiedete ad ogni bambino di scegliere, tenendolo segreto, un numero qualsiasi.
Voi indovinerete ogni numero segreto, facendovi dire da ogni bambino in quante e in quali colonne esso si trova.
Vi basterà fare la somma dei primi numeri delle colonne che ogni bambino vi indicherà. Tale somma è il numero segreto.
E se un bambino vi indicherà tutte e cinque le colonne?
Allora, non vi occorrerà eseguire la somma dei cinque numeri, poichè solo il 31 è visibilmente presente in tutte le colonne.
Sembra facile
Se tre gatti ammazzano tre topi in tre minuti, quanto tempo impiegheranno cento topi ad ammazzare cento gatti?
(Non li ammazzeranno mai neppure in cento anni, perchè i topi non ammazzano i gatti, ma viceversa)
Se tre gatti ammazzano tre topi in tre minuti, quanto tempo impiegano cento gatti ad ammazzare cento topi?
(Tre minuti, poichè il rapporto gatto – topo resta invariato, cioè di uno a uno).
Una stella di monete
Hai 12 monete tutte uguali; sapresti collocarle in modo da ottenere sei file di quattro monete ciascuna?
Risposta:

Curiosità sui numeri
Il 100 si può scrivere ripetendo 5 volte la stessa cifra:
100 = 111 – 11
100 = 3 x 33 + 3/3
100 = (5 + 5 + 5+ 5) x 5
La differenza è sempre 396
Dire a un bambino di scrivere la serie dei numeri dispari da 1 a 9. Così:
1 3 5 7 9
Fargli scegliere poi, a suo piacere, tre cifre consecutive e formarne un numero, ad esempio 357.
Rovesciare ora il numero ottenuto: 753.
La differenza tra i due numeri così ottenuti è 396.
Prova e verifica con altre cifre. Lo stesso fatto si verifica con la serie dei numeri pari da 0 a 8. Verifica con numeri da te scelti. Ricorda che le cifre devono essere consecutive. Ripeti il gioco coi tuoi compagni.
La gara della memoria
Disponiamo in ordine dieci oggetti diversi (una matita, un orologio, una caramella, un paio di forbici, un turacciolo, una gomma, una noce, ecc…) sopra un foglio di carta numerato dall’1 al 10, in modo che ad ogni numero corrisponda un oggetto.
Chiamiamo un bambino e facciamogli osservare il foglio per un minuto. Poi nascondiamogli il foglio e chiediamogli di ripeterci esattamente il nome e l’ordine degli oggetti osservati. Ogni oggetto esattamente ricordato gli farà guadagnare un punto. Si può ripetere il gioco in forma di gara, con più bambini.
Il gioco della mano svelta
I bambini vengono divisi in due gruppi di uguale valore fisico. I gruppi si allineano in fila su due linee parallele alla distanza di 8 – 10 metri. Si traccia una linea vistosa, nel mezzo, parallela alle precedenti, e si fa un piccolo segno al centro, sul quale può venir posto un fazzolettino o un altro oggetto di tessuto. I bambini porteranno uno stesso numero a due a due (uno per fila). Al comando, ad esempio “Pronti i numeri 5!”, i due 5 usciranno di corsa con l’impegno di cogliere l’oggetto e dubito fuggire senza toccarsi. Se uno riesce, fa vincere un punto alla propria squadra. Se uno si fa toccare, pur avendo preso l’oggetto, perde; se uno tocca l’avversario prima che questi prenda o tocchi l’oggetto, perde.
Questo gioco esercita l’attenzione visiva dei bambini e promuove l’esercizio del loro riflessi. Può essere eseguito sia all’aperto sia in palestra.
I raccoglitori
Gruppi di tre o più bambini in fila indiana si dispongono su di una linea tracciata sul terreno. Essa segnerà la partenza e l’arrivo.
Di fronte ad ogni gruppo (a 10 metri circa) viene tracciata una circonferenza (50 cm di diametro): dopo di essa ve ne saranno segnate altre tre o quattro alla distanza di 4 metri l’una dall’altra.
In ogni cerchio sarà racchiuso un oggetto (cappello, fazzoletto, pezzo di legno, ecc…).
Al via, il giocatore numero 1 di ogni gruppo correrà a prendere uno alla volta gli oggetti contenuti nelle singole circonferenze e li deporrà in un limite di terreno segnato sulla linea di base.
Quando il numero 1 avrà terminato il suo compito, toccherà il compagno numero 2, che partirà per riportare ad uno ad uno gli oggetti nella posizione primitiva.
Il numero 3 toccato dal numero 2 li riporterà alla base. E così di seguito. Vince il gruppo che riuscirà a far giungere prima il suo ultimo giocatore.
Gli oggetti devono essere deposti, non lanciati, entro la circonferenza.
I giocatori non potranno partire dalla base senza esser stati toccati dal proprio compagno sulla base stessa.

