Esercizi per la classificazione di triangoli e quadrilateri, adatti alla classe quarta della scuola primaria.
Classificazione dei triangoli
Stabilisci se è possibile costruire un triangolo con tre strisce di carta aventi le misure sotto indicate. In caso affermativo specifica accanto come risulta il triangolo rispetto ai lati.
Con le strisce lunghe: cm 10, cm 12, cm 15, si può costruire un triangolo?_________
Come?________________________
Con le strisce lunghe: cm 4, cm 7, cm 11, si può costruire un triangolo?_________
Come?________________________
Con le strisce lunghe: cm 8, cm 8, cm 10, si può costruire un triangolo?_________
Come?________________________
Con le strisce lunghe: cm 18, cm 10, cm 10, si può costruire un triangolo?_________
Come?________________________
Con le strisce lunghe: cm 14, cm 14, cm 14, si può costruire un triangolo?_________
Come?________________________
Con le strisce lunghe: cm 3, cm 4, cm 5, si può costruire un triangolo?_________
Come?________________________
Con le strisce lunghe: cm 3, cm 3, cm 4, si può costruire un triangolo?_________
Come?________________________
Quadrilateri
Prendiamo quattro strisce di cartoncino e colleghiamo i loro estremi in modo che nessuna striscia intersechi le altre. Otteniamo una figura con quattro lati e quattro angoli detta quadrilatero o quadrangolo.

Il quadrilatero non è una figura rigida e indeformabile come il triangolo: si può trasformare in altri quadrilateri aventi gli stessi lati ma non gli stessi angoli, e quindi di forma diversa.
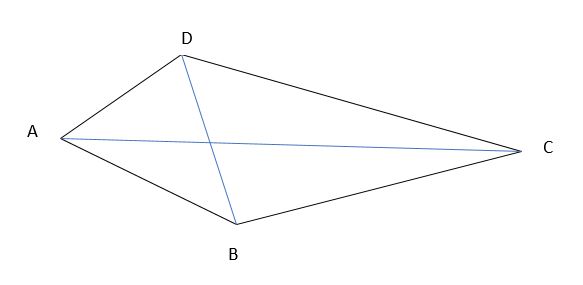
I segmenti che congiungono due vertici opposti del quadrilatero si chiamano diagonali. In ogni quadrilatero si possono tracciare due diagonali.
Nella figura ABCD è un quadrilatero: AC e BD sono le diagonali; A, B, C, D sono i vertici; il lato AB ha per opposto il lato CD; il lato AD ha per opposto il lato BC.
Rappresentiamo con un grafico l’intera famiglia dei quadrilateri:
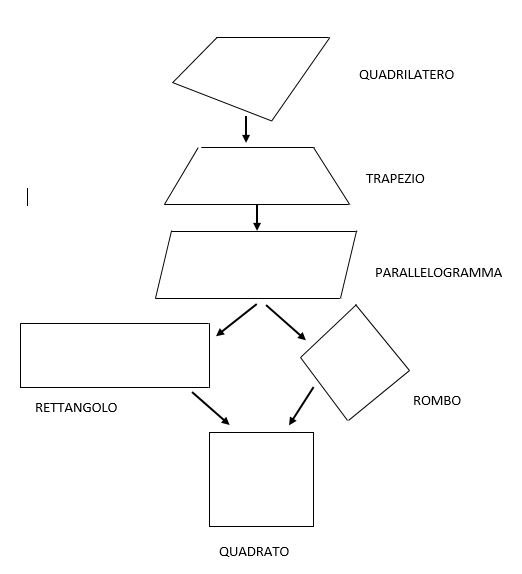
Il perimetro dei quadrilateri si trova sommando la misura dei rispettivi lati.
Classificazione dei quadrilateri
Prendi quattro strisce di cartone forate agli estremi e collegandole tra loro mediante dei ferma-campione, costruisci un quadrilatero articolato.
Con quattro strisce prese a caso, è sempre possibile costruire un quadrilatero?
Stabilisci se con quattro strisce aventi le misure sotto indicate puoi costruire un quadrilatero:
cm 6, cm 4, cm 5, cm 10.
Si può costruire un quadrilatero? ______________
dm 2, cm 8, cm 6, cm 5.
Si può costruire un quadrilatero? ______________
cm 6, cm 9, dm 1, dm 2.
Si può costruire un quadrilatero? ______________
cm 3, cm 3, cm 3, cm 3.
Si può costruire un quadrilatero? ______________
cm 3, cm 3, cm 3, cm 10.
Si può costruire un quadrilatero? ______________
cm 5, cm 5, cm 4, cm 4.
Si può costruire un quadrilatero? ______________
cm 3, cm 4, cm 3, cm 4.
Si può costruire un quadrilatero? ______________
cm 20, cm 8, cm 8, cm 4.
Si può costruire un quadrilatero? ______________
cm 6, cm 10, cm 5, cm 3.
Si può costruire un quadrilatero? ______________
Costruisci con 4 strisce un quadrilatero articolato quindi disponilo in modo da ottenere un trapezio.
Quando un quadrilatero si chiama trapezio?
Costruisci un rettangolo servendoti di 4 strisce a due a due uguali. Come devono essere disposte le 4 strisce per ottenere un rettangolo?
Tenendo fisso un lato esercita una leggera pressione su uno dei lati ad esso consecutivi: che cosa ottieni?
il rettangolo costruito e le figure ottenute nella trasformazione hanno lo stesso perimetro?
Costruisci un quadrato servendoti di quattro strisce uguali; tenendo fisso un lato ed esercitando una leggera pressione su uno dei lati ad esso consecutivi, il quadrato si trasforma in tanti rombi. Il quadrato costruito ed i rombi hanno lo stesso perimetro?
Come si chiamano i quadrilateri che hanno i lati a due a due paralleli? Come sono inoltre tra loro i lati paralleli?
Quali sono i quadrilateri che hanno le diagonali uguali?
Quali sono i quadrilateri che hanno le diagonali perpendicolari tra loro?
Disegna un trapezio isoscele, un trapezio rettangolo, un trapezio scaleno e traccia le loro diagonali. In quale dei tre trapezi disegnati le diagonali sono uguali?
Disegna un trapezio isoscele, un trapezio rettangolo ed un trapezio scaleno e traccia le distanze tra le basi, cioè le altezze dei trapezi. In quale dei tre trapezi disegnati l’altezza coincide con un lato?
Perimetro dei quadrilateri
Qual è il perimetro di questo parallelogramma?
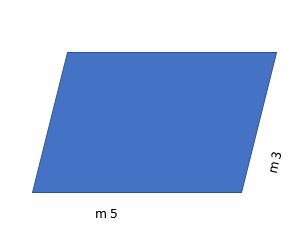
m (5+3+5+3) = m 16 (perimetro del parallelogramma)
Oppure:
m (5+3) x 2 = m 16 (perimetro del parallelogramma)
Qual è il perimetro di questo quadrato?

m (7×4) = m 28 (perimetro del quadrato)
Qual è il perimetro di questo rettangolo?
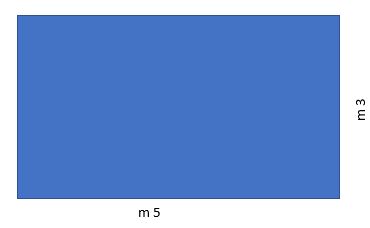
m (5+3+5+3) = m 16 (perimetro del rettangolo)
Oppure:
m (5+3) x 2 = m 16 (perimetro del rettangolo)
Qual è il perimetro di questo rombo?
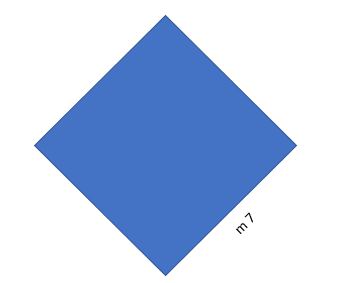
m (7×4) = m 28 (perimetro del rombo).
Troviamo il perimetro del nostro banco, della nostra aula, del corridoio, del cortile, ecc. (lavoro a gruppi).
Il trapezio
Costruito un quadrilatero con le quattro strisce di cartone, possiamo disporle in modo che due di esse risultino parallele: otterremo così un trapezio.

Il trapezio infatti è un quadrilatero che ha due paralleli. I due lati paralleli AB e DC (vedi figura) si dicono basi del trapezio; la distanza EF tra le due basi si dice altezza del trapezio.
Se i lati obliqui (i due lati non paralleli) sono uguali, il trapezio si dice isoscele: se uno dei lati non paralleli fra di loro è perpendicolare alle basi, il trapezio si dice rettangolo; esso ha due angoli retti.
Il parallelogrammo
Se nel trapezio costruito con le quattro strisce di cartone teniamo fissa la posizione delle basi e di un lato obliquo, e permettiamo all’altro lato obliquo di ruotare attorno ad un estremo della base minore, otteniamo tanti trapezi. Ad un certo punto il lato mobile si dispone parallelamente al lato opposto: il trapezio si è trasformato in un quadrilatero particolare che ha i lati a due a due paralleli: il parallelogrammo.

Il parallelogrammo è infatti un trapezio particolare ed ha:
– i lati opposti paralleli ed uguali
– gli angoli opposti uguali a due a due
– le diagonali che si tagliano scambievolmente per metà.
Il rettangolo
Il parallelogrammo è una figura mobile. Esercitando una leggera pressione su un lato, tenendo fermo uno dei lati ad esso adiacenti, il parallelogrammo si trasforma in tanti parallelogrammi diversi.
Osserva che gli angoli variano di ampiezza, rimanendo però uguali a due a due, finché, ad un certo punto, diventano tutti uguali e retti; otteniamo così un rettangolo, cioè un parallelogramma con tutti gli angoli uguali, retti.

Il rettangolo è un parallelogramma particolare avente:
– i lati opposti uguali e paralleli
– gli angoli tutti uguali e retti
– le diagonali uguali che si dimezzano scambievolmente.
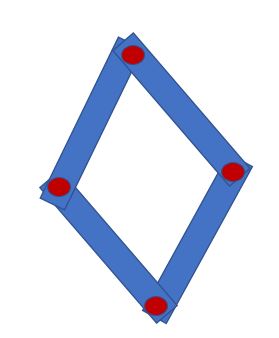
Il rombo
Abbiamo visto che il parallelogramma con tutti gli angoli uguali è il rettangolo. Il parallelogrammo con tutti i lati uguali è il rombo. Le diagonali dividono il rombo in quattro triangoli rettangoli uguali.
Il rombo è un parallelogramma particolare con:
– i lati tutti uguali a due a due paralleli
– gli angoli opposti uguali
– le diagonali perpendicolari che si dimezzano scambievolmente.
Il quadrato
Il rombo, come tutti i quadrilateri, è una figura mobile. Esercitando una leggera pressione su un lato e tenendo fermo uno dei lati ad esso adiacenti, esso si trasforma in tanti rombi diversi.
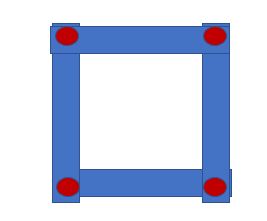
Ad un certo punto i lati si dispongono perpendicolarmente tra loro: abbiamo così ottenuto un quadrato, cioè un rombo con tutti gli angoli retti. Il quadrato è un rombo particolare che ha:
– i lati tutti uguali, a due a due paralleli
– gli angoli tutti uguali e retti
– le diagonali uguali, perpendicolari fra loro, che si dimezzano scambievolmente.
Problemi
– Un presepe ha la base quadrata il cui lato è di m 3. Qual è il perimetro della base del presepe?
– Disegna un rettangolo con le dimensioni di cm 8 e cm 4. Quanti centimetri misura il perimetro?
– Disegna un quadrato con il lato di cm 8. Quanti centimetri misura il perimetro?
– Luisa ricama su una tovaglietta un rombo con il lato di cm 25. Quale sarà la lunghezza del ricamo?
– Calcola il perimetro di un parallelogramma che ha un lato di cm 20 e l’altro di cm 16.
