Aste numeriche Montessori – SOMME DI PROGRESSIONI ARITMETICHE. Come già accennato qui
coi ragazzi più grandi, nello studio dell’algebra, possiamo tornare ad utilizzare un materiale che hanno conosciuto quando avevano circa 4 anni: le aste numeriche.
Se non disponete del materiale, potete utilizzare queste aste da stampare, plastificare e ritagliare.
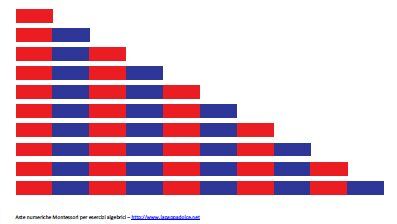
Al livello della Casa dei Bambini, si disponevano le aste di lunghezza graduale una sotto l’altra, in modo che risaltassero le diverse lunghezze e i loro rapporti.
Poi, uno degli esercizi consisteva nel collocare l’asta più corta a fianco della penultima, poi l’asta del 2 accanto all’asta dell’8, l’asta del 7 accanto all’asta del 3 ecc… in modo da ottenere aste uguali a quella del 10. Solo l’asta del 5 non aveva compagno, indicando perciò la metà di 10.

In questo modo si ottenevano cinque aste di valore 10 e una di valore 5: il conteggio di tutte le unità contenute nelle aste era così facilitato dalla loro stessa disposizione, che rappresentava la moltiplicazione 10×5=50 e l’addizione 50+5=55
Lo stesso concetto può essere rappresentato su carta quadrettata, in questo modo:
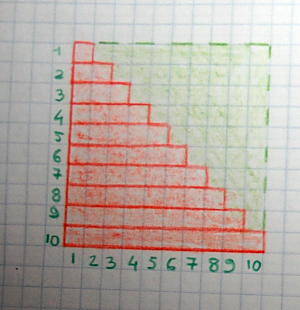
ottenendo un quadrato che misura 10×10 (10²).
Disponendo poi i segmenti in questo modo:
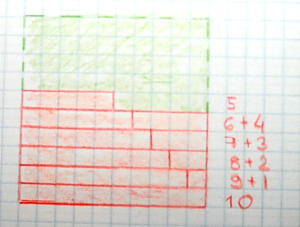
si arriva ad occupare metà del quadrato iniziale, ottenendo 5 righe di valore 10 l’una sull’altra, cioè 10²/2, ma avanza una mezza riga, un valore 5 ossia 10/2.
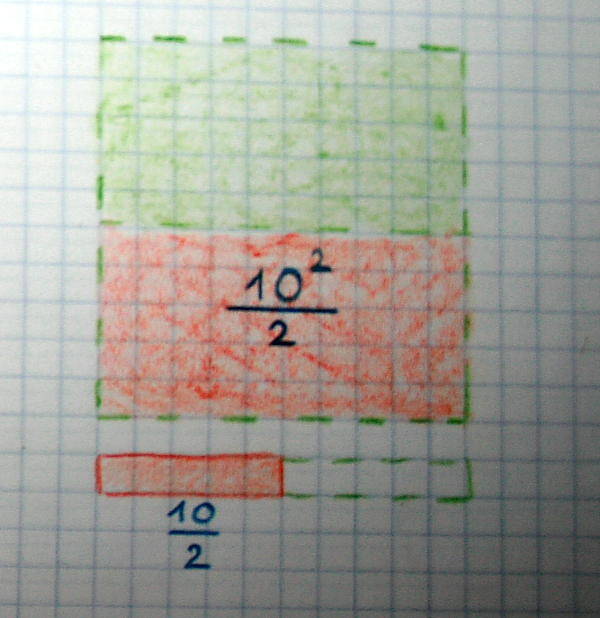
Considerando il 10 come maggior numero raggiunto nella serie naturale data dalle aste, si deduce che la somma della serie naturale dei numeri è uguale alla metà del quadrato di 10 + la metà di 10
1+2+3+4+5+6+7+8+9+10 =
= 10²/2 + 10/2 =
= (10²+1o)/2 =
= (100+10)/2=
=110/2 = 55
La stessa cosa di verificherà procedendo oltre al 10, collocando sempre l’1 vicino alla penultima quantità che differisce dalla maggiore per una unità e così via per le altre. Questo è ad esempi quello che succede prendendo in considerazione il numero 16:
16²/2 + 16/2
da cui
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16 = (16² + 16):2 = (256+16):2 = 272:2 = 136
Questo procedimento risulta molto più semplice che non addizionare un numero dopo l’altro, e la disposizione geometrica facilita moltissimo.
Se si dovessero addizionare i numeri da 1 a 100, la semplificazione sarebbe ancora più evidente. Invece di eseguire l’addizione:
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20+21+22+23+24+25
+26+27+28+29+30+31+32+33+34+35+36+37+38+39+40+41+42+43+44+45+46
+47+48+49+50+51+52+53+54+55+56+57+58+59+60+61+62+63+64+65+66+67
+68+69+70+71+72+73+74+75+76+77+78+79+80+81+82+83+84+85+86+87+88
+89+90+91+92+93+94+95+96+97+98+99+100=
basta procedere con questo semplice calcolo:
100²/2 + 100/2 = 10000/2 + 1oo/2 = 5000+50 = 5050
Questa semplificazione può essere applicata a qualsiasi grande numero, solo il calcolo può diventare più laborioso.
Per dare perciò a questo procedimento un carattere generale, che può essere applicato ad ogni addizione di numeri disposti secondo la serie naturale, si usa la lettera n (numero): è l’ultimo numero della serie. Abbiamo così la seguente formula:
1+2+3+…+n = (n² + n) : 2
Se vogliamo che i ragazzi arrivino con entusiasmo ad una formula algebrica, dice Maria Montessori, non dobbiamo spiegargliela, nè cercare di attirare la sua attenzione su di essa: conviene invece non insistere. Può essere necessario ripetere quello stesso esercizio cui si dedicava quando aveva 4 anni: lo spostamento delle aste; ripetere queste esperienze col disegno, con le liste, ecc… In questo modo, improvvisamente, l’idea prende forma e la formula che la esprime non solo apparirà interessante, ma anche necessaria, come è indispensabile il linguaggio per esprimere le idee e comunicare.
L’algebra che ricorre all’alfabeto è, con le sue formule, il linguaggio delle idee matematiche.
Quando i ragazzi arrivano a comprenderne il significato, si sviluppa in loro la tendenza a cercare, fra le esperienze fatte, idee che possano esprimersi mediante formule algebriche.
